この記事では伝達関数に基づく制御について1つの記事にまとめます。伝達関数に基づいた周波数領域での制御の個々のトピックの詳細を説明した記事へのリンクは都度貼っています。
- 伝達関数と基本事項
- ラプラス変換
- 伝達関数の定義
- ブロック線図
- 極と零点について
- 部分分数分解による信号要素の分解
- ボード線図
- ラウスの安定判別法
- ナイキスト線図と安定判別法
- PID制御
- 内部モデル原理
- 制御系のむだ時間
- 制御工学チャンネル内の伝達関数に基づく制御の関連ページ
伝達関数と基本事項
制御工学における仕様
制御では様々なタイプの制御対象や制約条件があります。また、達成すべき目的も様々です。しかし、ざっくりとした目的は似ている部分もありますし共通の変数設定があります。ここでは、その全体像について触れます。

まず、制御では以下の2つが主要な目的となります。
- 出力信号の指定された設定値への維持(レギュレーション)
- 出力信号の目標信号への追従(トラッキング)
レギュレーションでは、外乱等の影響下でも出力信号が一定に維持されるようにフィードバック制御を行います。
トラッキングでは、時間的に変化する目標値の動きに出力信号を合わせます。特に変化の速い目標信号への追従を行う場合には、制御則によって性能の良し悪しが大きく変わってきます。
以下の記事では信号と実装プロセスについての説明を行っています。制御に用いられる記号や設計・実装プロセス、学問としての役割について触れています。
ラプラス変換
ラプラス変換を用いることで、微分方程式の解が代数演算により導出できるようになります。まず、信号のラプラス変換の並びに逆ラプラス変換について述べたいと思います。ラプラス変換の定義を以下に示します。信号が時間の関数として
と与えられた場合、そのラプラス変換は
\begin{equation}
F(s):=\lim_{T\rightarrow\infty}\int_0^T f(t)e^{-st}dt
\end{equation}
で与えられます。このとき、を「
のラプラス変換」と言います。ここで、極限の記号を省略するとラプラス変換は次のように記載されます。
\begin{equation}
F(s)=\int_0^\infty f(t)e^{-st}dt
\end{equation}
このうち、指数関数のラプラス変換は制御工学において特に重要ですので、実際に求めてみることにします。
は単位ステップ関数と呼ばれ、以下のように定義されます。
\begin{equation}
{\bf{1}}(t) = 1; t \geq 0, {\bf{1}}(t) = 0; t < 0,
\end{equation}
指数関数だけでなく、様々な信号のラプラス変換を知ることは有用です。
以下の記事ではラプラス変換表や、特性について述べ、システムの伝達関数と極・零点について触れています。
伝達関数の定義
ここでは、対象システムの伝達関数を
と表記し、その対象に対する応答を表示します。伝達関数は入力のラプラス変換と出力のラプラス変換の比として与えられます。
\begin{equation}
G(s) = \frac{a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 }{b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0}
\end{equation}
ここで、は自然数であり、分子および分母は
に関する多項式です。各多項式における係数
および
は実数で与えられます。ここでは、システム
の極
は安定極であることを仮定して話を進めます。
以下の記事では、相対次数が0, 1, 2の3パターンの伝達関数を用意し、それらのステップ応答を示しています。
極零相殺については以下の記事でまとめています。
ブロック線図
ブロック線図は、システムの全体像を図的表現するために用いられます。その構成要素はブロックおよび矢印線であり、ブロックは要素やシステムを表現するのに用いられ、矢印は信号の流れを表現します。最も簡単なブロック線図は以下のように与えられます。

このとき、伝達関数表現されたシステムについて次式が成り立ちます。
\begin{equation}y(s) = G(s)u(s)\end{equation}
ブロック線図を用いた表現は様々な対象システムについて行われますが、ブロックの構成要素と全体像を結びつける際には、伝達関数表現されたシステムを利用すると便利です。このことは後述します。
以下の記事では、個々のブロックが伝達関数として与えられた場合について議論を展開し、ブロック線図における決まり事を紹介します。
極と零点について
ここでは、システムの伝達関数を
と表記し、その伝達関数固有の性質について考えます。
\begin{equation}
G(s) = \frac{a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 }{b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0}
\end{equation}
ここで、は自然数であり、分子および分母は
に関する多項式です。各多項式における係数
および
は実数で与えられます。
の分母多項式は
\begin{equation}
b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0
\end{equation}
であり、分子多項式は
\begin{equation}
a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0
\end{equation}
です。ここで、分母多項式を用いて
\begin{equation}
b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0=0
\end{equation}
を考えます。上式の根は個あり、それらを
と表記します。
には実数根だけでなく共役複素数となる根も含みます。同様に、分子多項式を用いて
\begin{equation}
a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 = 0
\end{equation}
を考えます。このとき、上式の根は個あり、それらを
とします。これも同様に共役複素数を含むことがあります。以上を踏まえ、
は次のように書き換えることもできます。
\begin{equation}
G(s) = \frac{a_m}{b_n}\frac{(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}
\end{equation}
システムの特性を考える上で上で示した表記は有用です。
をシステム
の極と呼びます。また、
をシステム
の零点と呼びます。特に、
の実部が
以上となる極を不安定極、
の実部が
以上となる零点を不安定零点と呼びます。
システムにおいて、
を次数といい、
と
の差を相対次数という。相対次数
が正の値のとき、
は厳密にプロパーといい、
が
のとき、すなわち
のとき双プロパーといいます。一般的な物理システムは厳密にプロパーもしくは双プロパーなシステムとして与えられます。
不安定零点と制御性能
以下が、不安定零点を持つ制御対象伝達関数の一例です。
伝達関数において、零点は [分子多項式] = 0 を満たす s であり、一つ目の対象の零点は であり、二つ目の対象の零点は
です。双方ともに実部が正の値を取っています。零点の中で一つでも不安定零点を持つと制御が極端に難しくなります。
以下の記事では、不安定零点を持つシステムの逆システムや逆応答、性能限界について触れています。
部分分数分解による信号要素の分解
制御工学において、ラプラス変換表により逆ラプラス変換を行うことで信号波形を得ます。信号のラプラス変換は の有理関数として与えられ、その信号が一次式や二次式の場合にはラプラス変換表により逆ラプラス変換で波形が求まります。他方、より高次の場合には、まず、有理関数として与えられた信号のラプラス変換に対して部分分数分解を施し、一次式もしくは二次式まで分解することにより、それぞれの項に対して逆ラプラス変換を施すことができ、信号波形が(時間の関数として)得られます。
簡単な部分分数分解と信号波形の例
ここでは、簡単な例を一つ示します。制御対象(伝達関数表現) に対して、単位ステップ入力(のラプラス変換)
を印加したとき、制御出力は次式で与えられます。
\begin{equation} y(s) = P(s) r(s) = \frac{1}{(s+2)s} \end{equation}
このとき、は次の形式に分解できます。
\begin{equation} \frac{A}{s+2}+\frac{B}{s}\end{equation}
ここで、、
とすると以下の等号が成り立ちます。
\begin{equation} \frac{1}{(s+2)s}=-\frac{1}{2}\frac{1}{s+2}+\frac{1}{2}\frac{1}{s}\end{equation}
ここで、を求めたいとき、上の式に基づいて、それぞれの項を逆ラプラス変換することで導出できます。
\begin{equation} y(t) = -\frac{1}{2} e^{-2t} + \frac{1}{2}\end{equation}
ここでは、分母多項式の次数が2のケースを扱っていますが、より高次の場合についても低次の項へと分解することで結果への見通しを良くすることができます。
実際の手法および例題については以下の記事でまとめています。応答計算や対角正準形の導出についての説明も行っています。
ボード線図
ボード線図の表現
どんな入力を印加すると、どんな出力が得られるかを考えます。伝達関数の
に
を代入してその大きさと角度を計算すれば、ある角周波数
を印加したときの出力
が次のように特徴づけられます。
\begin{equation}
y(t) = |G(j\omega)| \sin (\omega t + \angle G(j\omega) )
\end{equation}
ただし、上式は、制御対象が安定の前提下で、時間の経過とともに過渡的な信号が減少した後の最終的な定常出力を表している点に注意してください。
このとき、出力信号の振幅の大きさがで特徴付けられ、位相の遅れが
で特徴付けられます。入力振幅が二倍になれば出力振幅も当然二倍になりますが、ここでボード線図では、振幅比を表現することから入力の大きさは考えず、
で特徴付けられます。ボード線図は横軸を角周波数
として、ゲインと位相を表したものであり、伝達関数
さえ与えられれば、そこから容易に計算できます。通常、ゲインはデシベル表記するため
で与えられます。
ボード線図の例
システムの伝達関数がで与えられる場合について、そのボード線図を示します。
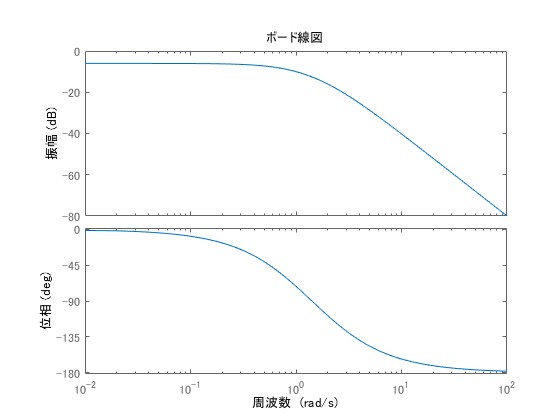
ボード線図の実例なども含めて以下の記事で詳解しています。
ラウスの安定判別法
ラウス表を構成し、その係数を確認することで安定性を調べることができます。
まず、は次のように与えられるものとします。
\begin{equation}s^n + a_{n-1}s^{n-1}+a_{n-2}s^{n-2}\cdots a_1 s + a_0\end{equation}
このとき、次のようにラウス表を構成します。
まず、および
の最初の2行については
の係数が高次から順に交互に並べていきます。
その後、の行に対応する
を計算し、
に対応する
を順に計算していきます。まず、
は
\begin{equation} b_1 = \frac{a_{n-1}a_{n-2} - a_{n-3} }{a_{n-1}}\end{equation}
と計算され、は
\begin{equation} b_2 = \frac{a_{n-1}a_{n-4} - a_{n-5} }{a_{n-1}}\end{equation}
と計算され、は
\begin{equation} b_3 = \frac{a_{n-1}a_{n-6} - a_{n-7} }{a_{n-1}}\end{equation}
と計算されます。上2行の係数に対するたすき掛けの要領での計算を順に進め、全ての演算を終えると次の行の計算をしていきます。そのように全ての演算を終えたとき、表の赤で示される列(最左列)の数列をラウス数列と呼びます。
このラウス数列の符号が反転しなければ安定であり、反転すると不安定です。そして、反転の回数が不安定極の個数に相当します。
以下の記事中に例題を含めて説明をしています。
ナイキスト線図と安定判別法
ここでは、閉ループ系の安定性について確認します。まず、および
が与えられているものとします。
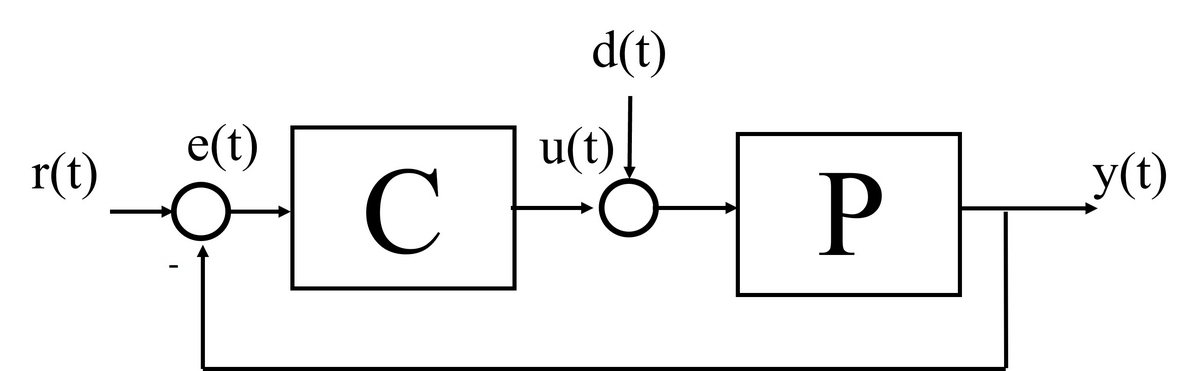
ここで、
\begin{equation} L(s) = P(s) C(s)\end{equation}
を一巡伝達関数と呼びます。閉ループ系の入出力特性は次のように与えられます。
\begin{equation} \frac{y}{r} = \frac{P(s)C(s)}{1+P(s)C(s)}\end{equation}
\begin{equation} \frac{y}{d} = \frac{P(s)}{1+P(s)C(s)}\end{equation}
閉ループ系の安定性を一巡伝達関数の不安定極の数と周波数応答データによって導きます。角周波数
が
から
の範囲で動いたとき、
の軌跡をナイキスト軌跡と呼びます。
ここでは、仮定として,
の間に不安定な極零相殺が無いものとします。安定判別法は以下の通りです。
安定性判別法
- 一巡伝達関数が極零相殺はないものと仮定する。
- ナイキスト軌跡
,
を描く。
- ナイキスト軌跡が点(-1+0j)の周りを時計回りに回る回数を
とする。
- 一巡伝達関数の極のうち、実部が正となる極の数を
とする。
の値が零であれば閉ループ系は安定であり、そうでなければ不安定である。
一巡伝達関数が安定な場合
まずは、一巡伝達関数が安定な場合について周波数応答データ
を複素平面上にプロットします。このとき、ナイキスト軌跡が点(-1+0j)の周りを時計回りに回る回数が零であれば安定です。
一巡伝達関数として
\begin{equation} L(s) = \frac{K}{(s+1)^3}\end{equation}
を与えます。
ここで、のとき、-1を周回する回数は図から零回であることがわかります。
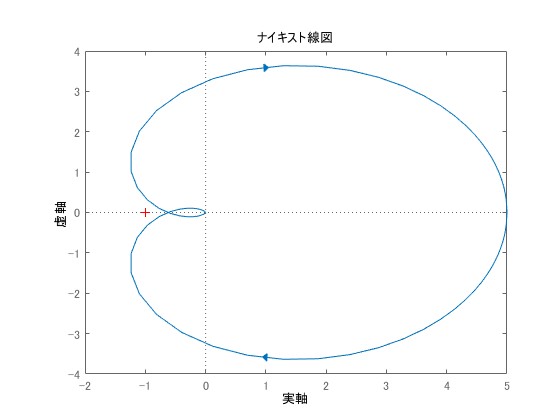
赤色の点を周回していません。の場合について、閉ループ系を組んでステップ応答を表示したものが以下の図です。
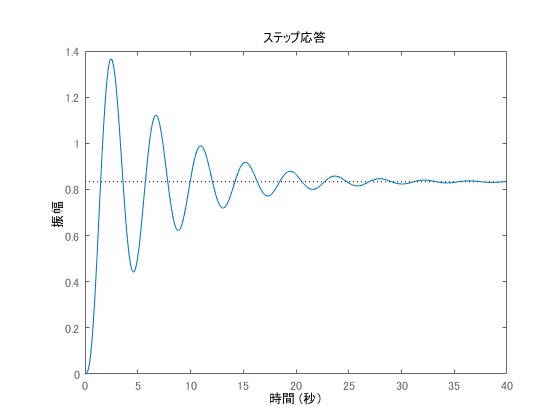
安定であることが応答から確認できます。他方、上記のナイキスト線図がであることから、
とした場合に赤の点(-1)を周回することが容易に予想できます。この他、不安定な例などは以下の記事で説明しています。
PID制御
PID制御器の内部構造
以下にPID制御器の構造について、その要素の説明をしていきます。PID制御は、基本的には単位フィードバックの構造をしており、その制御器部分が比例(P)、微分(D)、積分(I)で構成されています。
比例動作
まず P 動作 比例動作ですが、比例動作は出力と目標値との偏差を考えて、その偏差に比例係数をかけたものを制御入力として用います。
ボード線図は次のようになります。ゲインが周波数によらず一定値となっていることが わかります。

微分動作
次にD動作です。 D動作では偏差の変化量に比例した入力を構成します。 このためボード線図を見てやると低い周波数ではゲインが小さく、高い周波数ではゲインが大きくなります。

より変化に対して感度の高い入力を決定することになります。 そしてこのD動作とP動作を組み合わせたPD制御がよく使われます。
PD制御では、ゲインはある周波数まではフラットとなって、ある周波数以降では どんどん高い値になっていくボード線図の形状となります。このグラフの形状はPDゲインをどの値に設定するかによってシフトすることになります。

積分動作
最後にI動作です。 I動作では偏差信号を 考え、その積分値を考えます。この積分値に比例した入力を決定します。 このI動作に対してボード線図を見てやりますと、低い周波数では高いゲインとなり 高い周波数になるに従って、そのゲインが下がっていくような構成になっています。

この積分器を構成する時にはその初期値 を初期化することに注意する必要があります。 この積分器は目標信号がステップの場合には、目標信号と出力との偏差をゼロにする働きがあります。
PID制御器を構成すると次のようなボード線図の形状となります。

積分器の初期値は通常0としますが、その設定を考えずに実装すると想定外の応答になることがありますので注意してください。
コントローラーを設計する際には、まず出力がどのような応答になればよいかという ことを考える必要があります。その上でコントローラーの係数をどのような組み合わせにするかを考えることで、制御性能を良くしていくことになります。 出力の結果がどのような応答波形となるかは、制御対象の特性によっても依存しますし ゲインの係数によっても依存して変わってくることになります。
PID制御器の離散時間実装や、設計法については以下の記事で触れています。
内部モデル原理
出力信号を目標信号
に追従させる追従制御問題を考えます。
単位フィードバック系は次の図で与えられます。この単位フィードバック系を用いて内部モデル原理の説明を行います。

単位フィードバック系においてから
までの入出力伝達関数は、次式で与えられます。
\begin{equation}
G_y(s) = \frac{P(s)C(s)}{1+P(s)C(s)}
\end{equation}
ここでとすると
から
までの入出力伝達関数として
\begin{equation}
G_e(s) = \frac{1}{1+P(s)C(s)}
\end{equation}
を得るます。また、から
までの入出力伝達関数は次式で与えられます。
\begin{equation}
G_d(s) = \frac{P(s)}{1+P(s)C(s)}
\end{equation}
内部モデル原理(ステップ)
単位フィードバック系に対する追従問題を扱う場合における重要な原理が内部モデル原理であり、ステップ目標値の場合は以下のように与えられます。
- フィードバック系が内部安定であり、制御器が少なくとも一つの積分器を有するとき、ステップ目標値
およびステップ外乱
に対する単位フィードバック系の定常偏差は零となる。
ここでは、前提条件として制御対象が
に零点を持たないものとして話を進めます。単位ステップ
に対して偏差信号のラプラス変換
は次のように与えられます。
\begin{equation}
e(s) = G_e(s) \frac{r_0}{s} = \frac{1}{1+P(s)C(s)}\frac{r_0}{s}
\end{equation}
元のシステムが内部安定であり、部分分数分解した場合にとなるためには、次の条件を満たす必要があります。
\begin{equation}
\lim_{s=0} s\frac{1}{1+P(s)C(s)}\frac{r_0}{s} = \frac{1}{1+P(0)C(0)} r_0= 0
\end{equation}が積分器を持ち
と書き直せるとき
\begin{equation}
\lim_{s=0} s\frac{1}{1+P(s)C_0(s)/s}\frac{r_0}{s} = \lim_{s=0} \frac{s}{s+P(s)C_0(s)} r_0 = 0
\end{equation}
が自動で満たされます。よって、ステップ目標値に対して定常偏差が零となります。
他方、外乱に対する応答を確認します。外乱から出力までの伝達特性から
\begin{equation}
y(s) = G_d(s) d(s) = \frac{P(s)}{1+P(s)C(s)}\frac{d_0}{s}
\end{equation}
が得られます。このとき、部分分数分解した場合にとなるためには、次の条件を満たす必要があります。
\begin{equation}
\lim_{s=0} s\frac{P(s)}{1+P(s)C(s)}\frac{d_0}{s} = \frac{P(0)}{1+P(0)C(0)} d_0 = 0
\end{equation}が積分器を持ち
と書き直せるとき
\begin{equation}
\lim_{s=0} s\frac{P(s)}{1+P(s)C_0(s)/s}\frac{d_0}{s} = \lim_{s=0} \frac{sP(s)}{s+P(s)C_0(s)} d_0 = 0
\end{equation}
が自動で満たされます。よって、ステップ外乱に対して定常出力が零となります。
他の信号屋シミュレーションなどについては以下の記事で詳しく説明しています。
制御系のむだ時間
むだ時間は、入力信号がシステムに印加された後、印加した入力の影響が一定時間経過してから出力信号に反映されるような場合の応答開始までの時間差のことを表します。プロセス系や信号の伝送過程における遅延など様々な要因で生じます。制御入力をとし、むだ時間長さを
とすると、入力むだ時間を含むシステムの伝達関数表現は有理関数
を使って次のように表すことができます。
\begin{equation}y(s) = P(s)e^{-Ls} u(s)\end{equation}
と表現され、制御システムと表記される無限次元系として表されます。
むだ時間系の応答波形
まず、応答波形を確認してみます。むだ時間がないシステムとむだ時間を含むシステム
との比較図が以下の通りです。ただし、
とし、
としていますので、有理関数部分は全く同じです。ここでは
となっています。
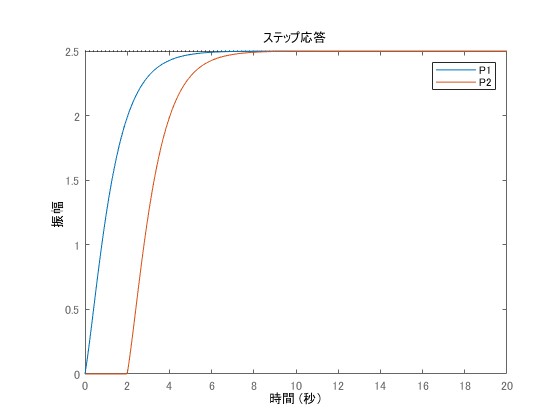

むだ時間系の応答波形を確認すると、各時刻の値が2秒づつ右にシフトしていることがそれぞれ確認できます。
むだ時間系に対する設計や近似表現については以下の記事で説明しています。
制御工学チャンネル内の伝達関数に基づく制御の関連ページ
動画ポータルサイト「制御工学チャンネル」内の伝達関数に基づいた制御へのリンクはこちらです。各教員ごとのページとしてまとまっています。
伝達関数に基づく制御
伝達関数に基づく制御・古典制御の書籍一覧
古典制御の本は様々にありますが、その中の一部を紹介します。
佐賀大学の佐藤先生らによる著書です。
杉江先生、藤田先生による著書です。学生時代はこの本で学びました。
荒木先生による著書です。
足立先生の制御工学のこころ(古典制御編)です。
制御工学の演習の書籍です。
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島寛 (システム制御 control-theory.com)
English Web Page
Hiroshi Okajima (Control Engineering control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
以上が伝達関数に基づく制御の記事全体をまとめた記事になります。本記事は以上です。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。




