この記事ではシステムの状態方程式表現(状態空間実現, State-Space Realization)についてまとめます。状態方程式に基づく制御において数理モデルの導出は最初のステップです。状態方程式の表現について説明した動画は最下部に置いております。ここでは、状態方程式表現に関する式の説明と制御システムの分類、状態空間表現の導出方法(モデル化、常微分方程式・伝達関数からの変換)について述べます。
なお、状態フィードバック制御の全体像は次の記事でまとめています。
状態空間実現
それではシステムの状態方程式表現について説明していきます。状態方程式表現は制御工学において重要な制御対象のモデル表現形式です。ここでまず状態方程式の主な記号について説明していきます。

tは時間であり、応答を表すグラフの横軸で用いることになります。x は状態ベクトル、uは制御入力、yは制御出力です。
状態方程式では状態ベクトルを使ってシステムのダイナミクスを表現します。n がシステムのは次数であり、この次数が状態ベクトルの要素数に対応します。また A,B,C はそれぞれ行列とベクトルであり Aは n次の正方行列です。
Bは入力が1個の場合は n次 の縦ベクトル、入力が複数の場合は行列形式になります。Cは出力が一つの場合はn 次の横ベクトル複数の出力がある場合は行列になります。
そして状態方程式は左辺に状態ベクトルの微分、右辺にAx+Buという以下の形で表現されます。
![]()
図ではn が3の例も示しています 。n が3の場合には、状態の要素数は3つになり、 A 行列は3×3の行列(ここでは可制御正準形)、B と C はそれぞれベクトル形式になります。状態ベクトルが縦長のベクトルなのでその微分値も縦長のベクトルになります。(以下は n = 3の例)
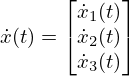
なお、本記事では連続時間状態方程式について説明していますが、離散時間の状態方程式もあり、以下の形式で記述されます。
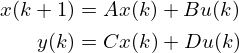
状態方程式の分類(時不変,時変,非線形)
次に状態方程式表現における制御システムの分類について説明します。
まず線形システムというのは先ほど示したようなA, B, C行列によって特徴づけられる形式になります。そして線形時不変システムと書いた場合は、この A, B, Cがそれぞれ固定の行列ベクトルとなっている場合を指しています。他方、線形時変システムという時にはこの A, B, C がそれぞれ時間の関数になっている場合を示しています。
基本的に線形システムといわれた時には線形時不変システムと思っておおよそ間違いないです。
次に非線形システムですが、非線形システムは一般的に図の下部ような形式で書かれます。このような形式で書けるものには線形システムのこの構造も含みますが、一般的に上部のシステムとは別形式で表します。

またこの非線形システムの中でも分類があります。右辺が f(x) + g(x)uと書かれている、uに関してアフィンな構造を持っている形式は非線形制御の分野で広く利用されている形式です。この他、ハンマシュタイン型非線形システムなどがあります。
数理モデリング
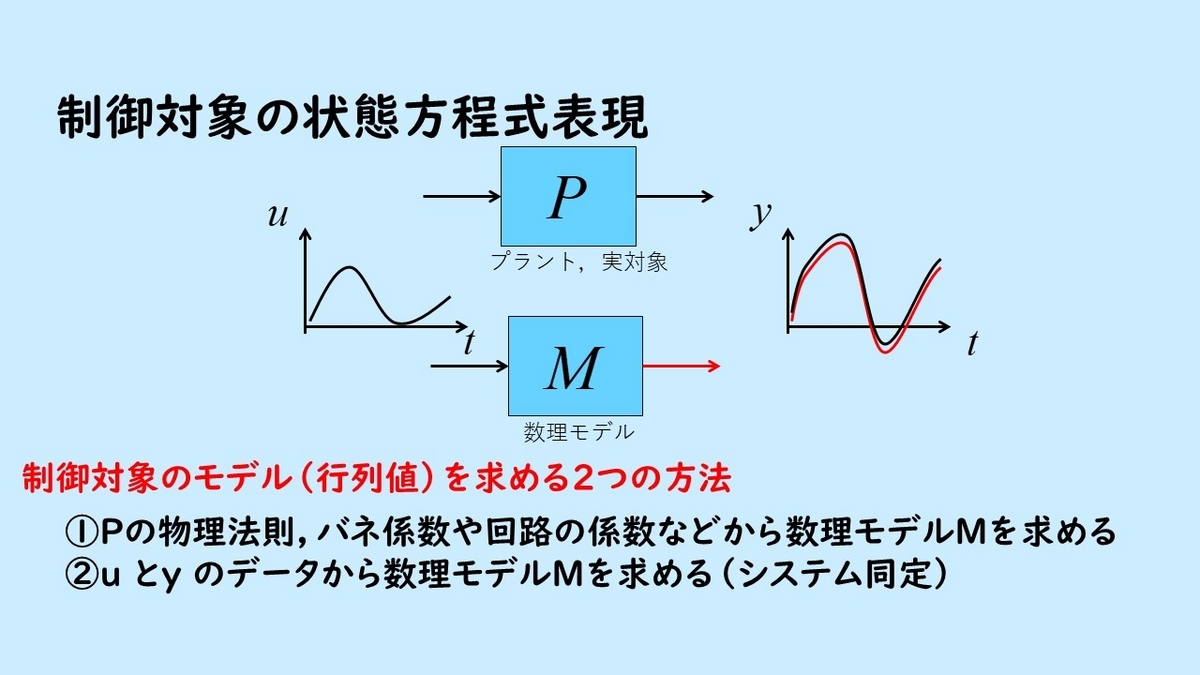
次に制御対象の状態方程式表現によるモデル化について考えます。通常、制御対象のモデルを求める際には2種類の方法を用います。ひとつは物理法則などから数理モデルを求める方法。もう一つは入力uと出力yのデータ列の組み合わせを利用することによって、数理モデルを求める方法です。これはシステム同定と呼ばれています。これらの手法によって、A, B, C のそれぞれの行列およびベクトルを求めることになります。
状態方程式と常微分方程式
次に2階の常微分方程式を状態方程式に変換する、変換の手法について説明します。
まずこのような常微分方程式を与えられた場合、z を状態のうちの1つ 、z の時間微分の状態のうちの2つ目、と定義すると、状態方程式表現は図のように可制御正準形と呼ばれる形式として求まります。
ただし、ここでは出力として z を用いた場合には、C = [1 0]となります。これが仮に z の時間微分値を出力信号としたい場合には、C = [0 1] とすれば良いです。

状態方程式と伝達関数
最後に伝達関数を状態方程式に変換するケースを紹介したいと思います。
例えばこのように伝達関数が与えられているときに、一つのアプローチとしてはこれを部分分数分解し、対角正準系呼ばれる一つの状態方程式表現に変換する方法があります。
部分分数展開することで 1/(s + a)の係数と、1/(s + b)の係数のそれぞれが求まります。求まった値はγ1、γ2としています
A,B,C の行列は図のように得られます。ここでは2次の例を示していますがより高次元の場合にも同じような流れでモデルを状態空間表現として得ることが可能です。

部分分数分解については次の記事で詳しく説明しています。
状態方程式表現に関する動画
以下は、状態方程式表現に関する動画になります。
本記事では、数理モデルの一つとして状態空間表現について述べました。状態空間表現の特徴や、分類、常微分方程式や伝達関数からの状態方程式の導出について説明しました。
次の記事では、状態方程式表現・状態空間表現されたモデルの可制御性、可観測性について説明しています。
モデルパラメータの入出力データからの導出にはシステム同定法が用いられます。
関連ページ(状態方程式)
>>制御工学チャンネル:500本以上の制御動画ポータルサイト Control Engineering Channel - 01-Prof.Okajima (control-theory.com)
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト