この記事ではシステムの可制御性・可観測性についてまとめます。まず,可制御性について述べたいと思います。なお,可制御性・可観測性について説明した動画へのリンクは最下部に置いています。
なお、状態フィードバック制御の全体像は次の記事でまとめています。
状態方程式表現

まず制御対象の状態方程式表現は上図のようになっています。まず状態方程式において、制御入力は、制御出力は
です。状態ベクトルは
と表現していて、その要素数は
個あります。
このようなシステムの次数のことをnという記号を用いて表していて、 n 次のシステムに対して 行列は
次の正方行列です。
は仮に1入力システムの場合には
次の縦長ベクトルで、入力数が多数ある場合は行列の形になります。
は
次の横ベクトルで、仮に出力数が多数ある場合には、行列の形になります。
システムの可制御性
まず可制御から説明をします。可制御性は、入力によって自由に状態を動かせるかを表現する指標であり、制御工学分野の重要事項の一つです。まず、可制御か可安定であれば状態フィードバックで安定が可能です。例えば、制御対象に対して、 という状態フィードバック制御を施す場合、これによって
\begin{equation} \dot x (t) = (A-BK)x(t) \end{equation}
で与えられる自律システムが得られます。この の固有値の実部が負であれば自律システムは安定になります。もし、システムが可制御もしくは可安定であるならば、そのようなことを実現する
が存在するといえます。
ここで可制御であれば可安定であるというのは成り立ちますが、逆に可安定であっても
場合によっては可制御にならないようなケースがあります。
例えばもともとが安定で、
が零ベクトルというケースでは、
を適当に与えてもシステムの安定性は保たれますが可制御ではなく、極を任意に配置するといったこともできません。
可制御であれば、適切なフィードバックゲインを与えることで
の極を任意に配置することができます。

図に示すように、ここで可制御性を調べるためには、可制御性行列Uc というものを用います。この行列は
、
、…と並べた行列になっています。仮にこの行列のランクが
であれば、このシステムは可制御になります。
次数ごとの可制御性行列
まず、 の場合は状態数 1 であり、
は次の形になります。
\begin{equation} U_c = B\end{equation}
このとき、が非零であれば
のシステムは可制御となります。
次に、 の場合です。状態数は2であり、
は次の形になります。
![]()
最後に、 の場合です。
は以下で与えられます。
![]()
入力数が1の場合は、行列サイズが になります。そのランクが
であれば可制御で、そうでなければ不可制御です。
次に、具体例を見ていきましょう。

例1: まず が2のシステムとしてA, B行列が図の左のように与えられている2入力のシステムを考えます。
の2次システムですので、可制御性行列
のランクが2であることから可制御になります。入力数が複数になると行列が正方でなく横長になります。
例2: 次の例としては としてA, Bが図の中央のように与えられている例を考えます。このケースでは、システムの次数は 3 です。ここで、可制御性行列のランクが 3 ありますので可制御となります。
なお、この場合の行列の対は可制御正準系と呼ばれる形式になっています。
例3: のシステムとして
が図の右のように与えられているケースを考えます。最後にこの3番目のケースですが、こちらは
のランクは2になります。そのため
であるのに対し、ランクが2であるため不可制御となります。
状態方程式の可観測性
次に可観測について説明します。可観測もしくは可検出であれば制御対象の全状態を状態オブザーバーによって推定することが可能です。ここで先ほどの可制御の場合と同様に可観測であれば、可検出であるという性質が成り立ちます。その逆に可検出であっても必ずしも可観測は成り立たないといえます。

ここで可観測性を調べるためには、可観測性行列を調べれば良いです。この可観測
行列は と縦に並べた行列になります。
次数ごとの可観測性行列
まず、 の場合は状態数 1 であり、
は次の形になります。
![]()
このとき、が非零であれば可観測になります。
次に、 の場合です。状態数は2であり、
は次の形になります。
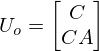
最後に、 の場合です。状態数は3であり、
は次の形になります。
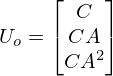
この行列のランクがであれば、可観測
未満であれば不可観測となります。ここでは示しませんが、可制御なシステムで可制御正準形があるように、可観測なシステムでは可観測正準形があります。
可制御性行列の場合と同様に、出力数が1であれば正方行列となりますが、出力数が2以上であると縦長の行列になります。
可制御・可観測に関する動画
最後に、可観測性に関する動画を示して終わりたいと思います。
関連ページ(可制御・可観測)
>>制御工学チャンネル:500本以上の制御動画ポータルサイト Control Engineering Channel - 01-Prof.Okajima (control-theory.com)
前の記事:
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。