この記事では状態方程式表現されたシステムの状態フィードバック制御についてまとめます。特に、極配置法によるゲイン設計と、極配置と性能との関係について触れています。最後に、制御シミュレーションや本記事の関連動画を置いておりますので併せてご覧ください。
なお、状態フィードバック制御の全体像は次の記事でまとめています。
状態方程式とフィードバック制御
制御対象の状態方程式表現
状態フィードバック制御は、図に示すように状態量に係数を掛けて、それを制御入力として制御する手法(制御則)になります。制御工学における基礎的な制御系設計理論の一つです。

状態フィードバックについて説明をします。状態方程式表現された制御対象が、このように与えられていて、制御入力が、制御出力が
となります。状態フィードバックでは、
という形で、制御入力は状態量に係数をかけたものとして入力されます。

上図に示されるものが状態方程式の主な記号になります。 は時間を表していて、
は状態ベクトル、
は入力、
は制御出力です。このシステムの次数は
という記号を用いて表していて、
は 1 以上の整数になります。
状態方程式表現の詳細はこちら
状態フィードバック制御と自律系
状態方程式として与えられるシステムに入力uを- Kx と与えることによって、以下の自律系が得られます。
ここで状態フィードバックを施したシステムのダイナミクスは、この行列 A-BK
によって決まります。
なお、制御則において、 でなく、
という表現や
という表現など、フィードバックゲインおよび制御則の表現形式が色々ありますが、ここでは
として進めます。
例えば、n = 3の場合は K は次のベクトル形式になります。
]
また、仮に同じ n = 3であっても、入力数が 2 の場合は K は次の行列形式となります。

極配置法により配置されたシステムの極と制御性能
極配置について説明する前に、まず極についての説明を行います。行列A-BKの固有値がフィードバック系の極であり、次の特性方程式
の根でもあります。フィードバックゲインKを定めると、それによって極の値がいろいろ変化します。
特選方程式の根、制御系の極、それぞれ等しいですので、(可制御であれば)制御系の極を自由に、いろいろといじることができます。

このフィードバックゲインの決定により、
の極を適切な場所に配置する、というのが極配置においては重要になってきます。
行列の固有値が極ということから、この極の数は全部で 個あります。また、全ての極が複素平面の左側にあれば漸近安定であり、これはゲイン
を設定する上での必要最低限の条件になります。
スカラシステムの極と応答
スカラシステム()の場合、
ともにスカラ値となります。極は
です。自律系は
であり、その解軌道は
で与えられます。の値が負であれば
の増加と共に
の値はゼロに収束していきます(安定)。他方、正の値であれば発散します(不安定)。
極と安定性
スカラシステムの場合と同様に でも、極の実部が負であれば零に漸近し、一つでも実部が正の極があれば発散します。システムが安定であるためには、全てのが極が複素平面の左側にある、というのが必要な条件になってきます。
それでは例題を見ていきましょう。ここでは すなわち3次のシステムの例を示します。
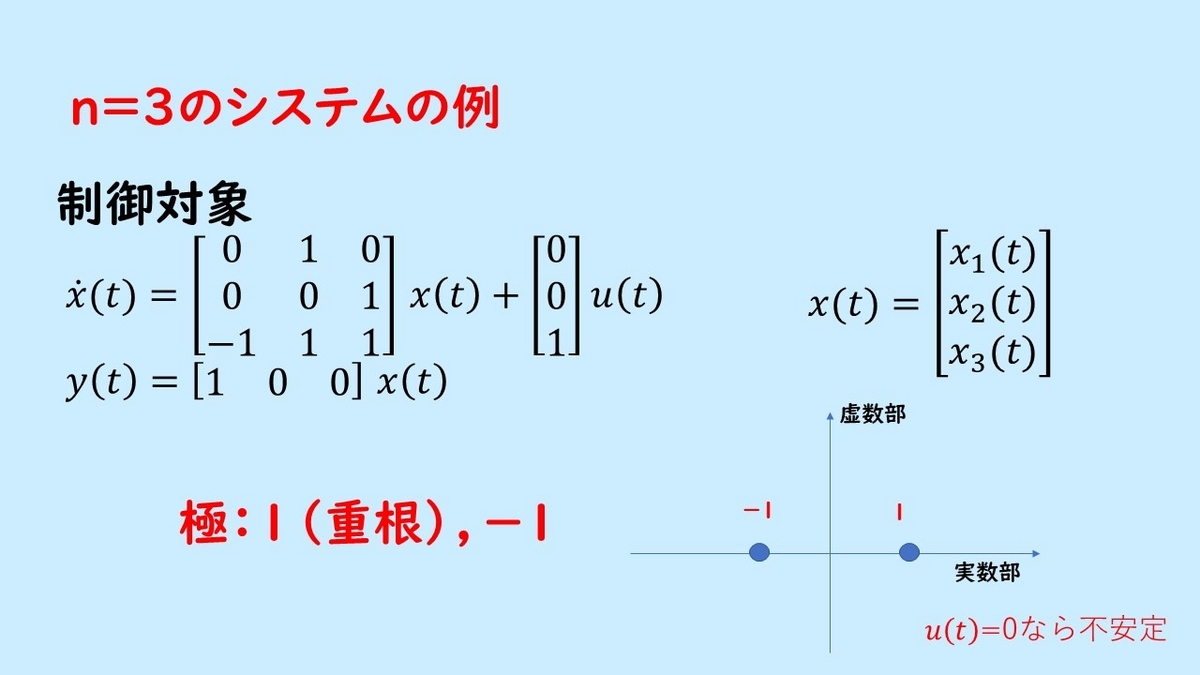
この制御対象は状態数が3個あり、システムの極である a 行列の固有値は1(重根)と-1となります。全ての極が左平面にはないので、仮にこの入力uを 0 とした場合にはこのシステムの状態が発散します。すなわち不安定システムになります。
次に状態フィードバック
]
を与えることで、極を-1,-2,-3とすることができます。この結果、元のシステムが不安定であっても、極配置により安定化ができます。

極配置と制御性能
極の実部と応答
次に極の配置(極の位置をどうするか)によって、どのような挙動の違いが出てくるかについて説明します。まず以下の図において、ゲイン2は極を虚軸寄り、この左半平面にはあるものの、虚軸寄りに配置して-0.5 -1 -2と配置したケースです。そして、極をより左側に配置して、-5 -6 -7としたものがゲイン3になります。そして、その極配置を実現するためのフィードバックゲインKはそれぞれ異なっています。

このとき、ゲイン3の極をより左側に配置した方が、早く原点に収束し、ゲイン2よりも早い応答を実現することができます。
状態数3のシステムに対して極配置法によりとした応答波形を青色とし、
とした応答波形をオレンジ色として以下に示します。
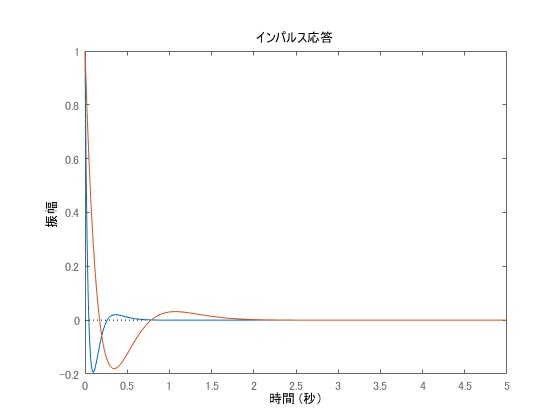
青色の方がより早く0に収束している様子がわかります。次に、極の一部のみを変更した数値シミュレーションを示します。青色がであり、オレンジ色が
です。このとき、一つの共役対の極の実部を0に近く配置したオレンジの方が応答がかなり遅くなっていることが確認できます。
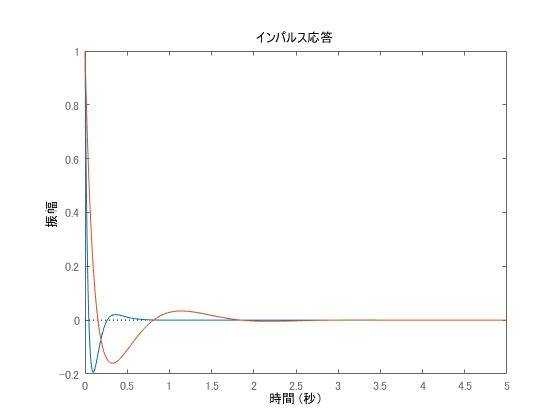
その他の数値シミュレーションは、下部の動画からも確認できます。
極の虚部と応答
次にゲイン4とゲイン5で実軸から遠い位置に配置した極と、近い位置に配置した極の比較を行います。
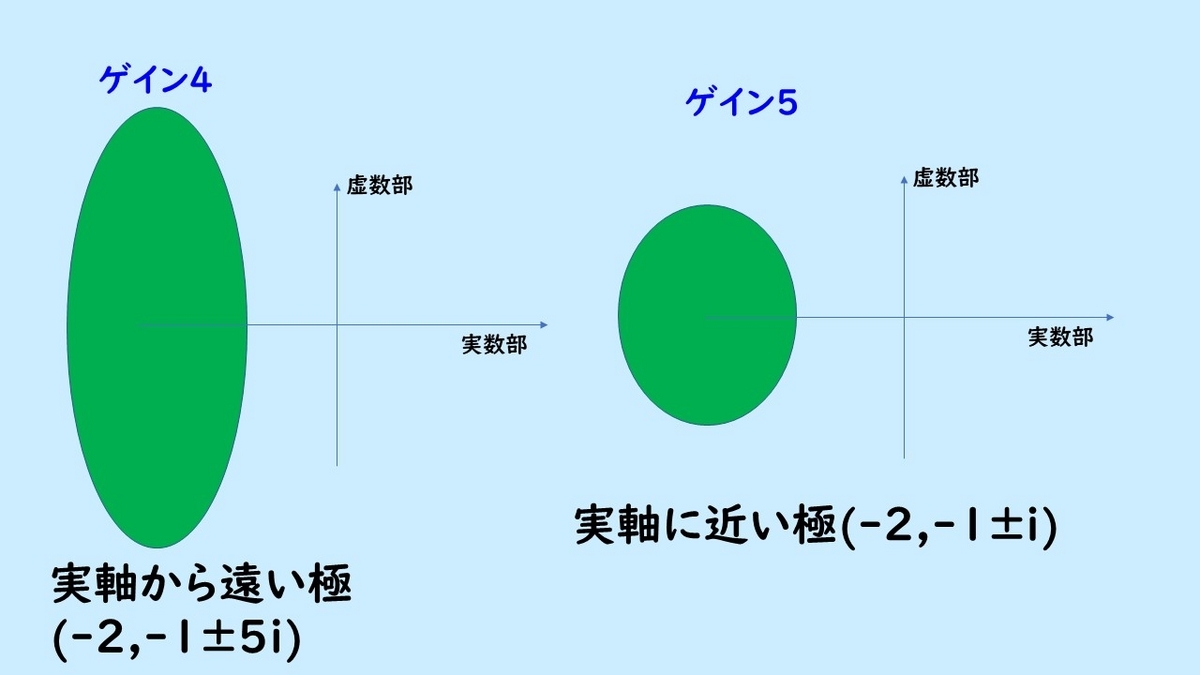
実軸から離した-2, -1± 5i に極を配置した場合は振動的な応答波形になります。次に実軸に近い位置に配置した場合、その場合には振動が少ないです。
実際に数値例を通してみてみようと思います。青色がであり、オレンジ色が
です。このとき、実部を変えずに虚部の値のみ変更している状態ですが、応答の振動性が高くなっていることがわかります。
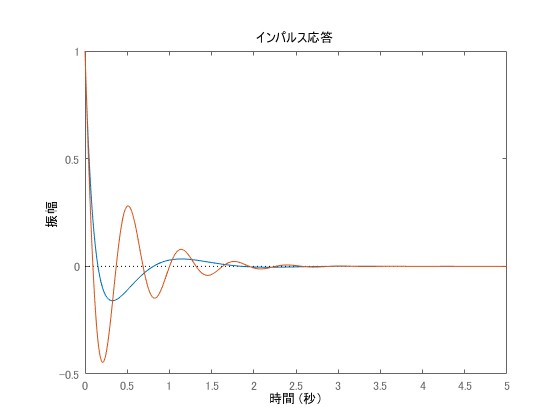
極と応答のまとめ
まず n 次 のシステムの極は全部で n 個あります。そして全ての極が複素平面上の左側にあれば、システムは漸近安定です。
極を配置するときに気をつけるのは、まず振動的にならないように、実軸から遠い位置に配置しすぎない、極の配置は実軸からあまり離しすぎない、というのが一つ重要になります。
また収束を速くする目的で虚軸からより左側に極を配置してやると、収束が早くなります。
その一方で、この虚軸からより離し過ぎると、入力信号の物理的な値が大きくなる傾向にありますので、システムに印加できる入力の範囲に従って、その配置を決める必要があります。
ほかにも、極の極同士の近さが近すぎないようにするなど、いろんな制約があります。
可制御正準形の極配置
それでは可制御正準系に対する極配置について説明していきます。制御対象が状態方程式表現された場合について、指定の極となるよう状態フィードバックゲインKを求める問題を考えます。このような問題を極配置問題と呼びます。
ここで制御入力uは、状態に比例係数をかけた形で
と与えられます。これによって制御出力を定めます。ここでは、制御対象が可制御であると仮定します。可制御の場合は可制御正準形に変換することができます。
可制御正準形の制御則と構造
それでは可制御正準系について見ていきます。まず2次の場合の可制御正準系の構造はこのようになっています。
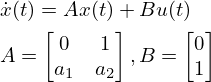
次に、3次の場合はこのようになります。
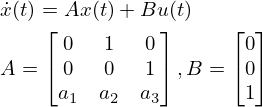
可制御正準系が与えられた場合、制御則u = -Kxを施した特性方程式は次のように与えられます。
2次の場合の特性方程式
3次の場合の特性方程式
それぞれにおいて、特性方程式の根が理想的な値になるように、係数Kを求めるだけでフィードバックゲインが得られます。例えば、制御対象が2次で、特性根(極)を-2, -1の二つに設定したい場合、理想的な特性方程式は
であり、これと係数が合うようにk1とk2を定めればフィードバックゲインが得られます。また、複素数を配置したい場合(-2±i)であれば
に合わせて係数4, 3に対応してを定めれば極配置できます。このように、極配置により制御システムの特性を決定できます。可制御でなければ一部の極については所望の配置ができないことに注意する必要があります。

状態フィードバック制御では、全ての状態量(状態ベクトルの要素)が計測できる場合に利用できます。他方、出力数が状態数より少ない場合は、オブザーバを組むことにより出力フィードバック制御系としてシステムを構成することになります。以上で本記事の説明を終わります。
実機実験とシミュレーション
倒立振子の実機実験を行った記事はこちらです。
MATLABシミュレーション
状態フィードバック制御のMATLABシミュレーションは以下のページでまとめています。
状態フィードバック制御の関連動画
以下は,状態方程式表現されたシステムの極と安定性について説明した動画になります。
以下は,状態方程式表現されたシステムの極配置について説明した動画になります。
MATLABシミュレーションによる極配置
関連ページ(極配置)
>>制御工学チャンネル:500本以上の制御動画ポータルサイト Control Engineering Channel - 01-Prof.Okajima-02 (control-theory.com)
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。