制御系設計において、伝達関数をベースとした理論展開が多くされています。伝達関数は周波数領域で対象の入出力特性を表現したものであり、表記としては、対象をとすると添え字
を用いて
のような形で表現します。このとき、
は、分子分母がそれぞれ
の多項式の形で表現されます。ここでは、伝達関数に基づく制御の基礎事項としてラプラス変換について説明します。さらに、伝達関数の特徴についても説明を行います。
信号のラプラス変換と逆ラプラス変換
ラプラス変換を用いることで、微分方程式の解が代数演算により導出できるようになります。まず、信号のラプラス変換の並びに逆ラプラス変換について述べたいと思います。ラプラス変換の定義を以下に示します。信号が時間の関数として
と与えられた場合、そのラプラス変換は
\begin{equation}
F(s):=\lim_{T\rightarrow\infty}\int_0^T f(t)e^{-st}dt
\end{equation}
で与えられます。このとき、を「
のラプラス変換」と言います。ここで、極限の記号を省略するとラプラス変換は次のように記載されます。
\begin{equation}
F(s)=\int_0^\infty f(t)e^{-st}dt
\end{equation}
このうち、指数関数のラプラス変換は制御工学において特に重要ですので、実際に求めてみることにします。
は単位ステップ関数と呼ばれ、以下のように定義されます。
\begin{equation}
{\bf{1}}(t) = 1; t \geq 0, {\bf{1}}(t) = 0; t < 0,
\end{equation}
指数関数だけでなく、様々な信号のラプラス変換を知ることは有用です。そのため、以下の表にラプラス変換表をまとめます。実際に成り立つことは定義式に従って確かめればよいでしょう。
ラプラス変換表
と
との関係を表しており、与えられた
から
を求めることをラプラス逆変換と呼びます。
特に、逆ラプラス変換は応答を計算するために重要であるため、表のうち主要な関数については暗記しておくのがよいと考えます。さらに、定義から導かれる様々な性質について以下にまとめます。特に性質1〜4は制御系の解析と設計において重要な役割を果たします。
(性質1)線形性
任意の複素数(実数を含む)に対して
が成り立つ。
(性質2)最終値定理
が
>0で収束するものとする。このとき、次式が成り立つ。
\begin{equation}
\lim_{s\rightarrow 0} s F(s) = \lim_{T\rightarrow \infty}f(T)
\end{equation}
(性質3)導関数に対するラプラス変換
>
(性質4)積分に対するラプラス変換
>
さらに、性質1〜4を含めて主要なものを以下の表にまとめます。
入出力信号と伝達関数
制御対象の入出力が与えられたとき、その伝達関数は、入力のラプラス変換
と出力のラプラス変換
の比として与えられ、次式で与えられます。
\begin{eqnarray}
P(s) = \frac{y(s)}{u(s)}
\end{eqnarray}
「出力のラプラス変換=対象の伝達関数×入力のラプラス変換」となります。仮に制御対象の伝達関数が既知で、入力信号のラプラス変換
も既知であれば、
の関係と、ラプラス変換表を用いることで、微分方程式を解くことなく応答波形を算出することが可能です。そのことを具体例で確認します。
制御対象をとすると、伝達関数では例えば以下のように表わされます。
\begin{equation}
P(s)=\frac{2}{s+1}
\end{equation}
そして、入力がステップ
の場合、出力
は
\begin{equation}
y(s)=\frac{2}{s+1}\frac{1}{s}
\end{equation}
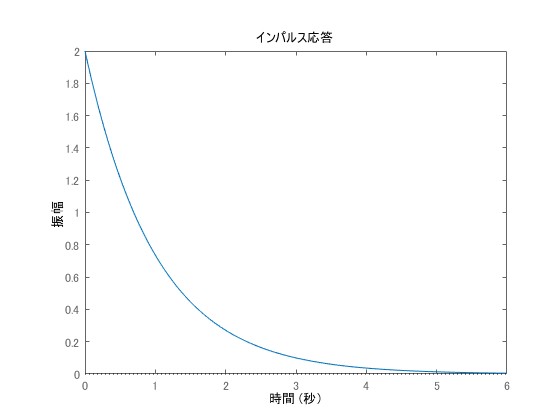
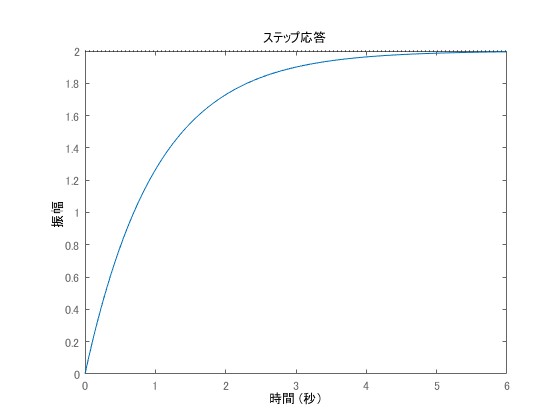
で表わされ、逆ラプラス変換することで出力信号が
\begin{equation}\label{s1}
y(t)=2-2\exp[-t]
\end{equation}
と表現できることがわかります。このとき、時刻では上式の右辺第2項は零となるため定常時には
となります。
システムの伝達関数と極と零点
ここでは、システムの伝達関数を
と表記し、その伝達関数固有の性質について考えます。
\begin{equation}
G(s) = \frac{a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 }{b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0}
\end{equation}
ここで、は自然数であり、分子および分母は
に関する多項式です。各多項式における係数
および
は実数で与えられます。
の分母多項式は
\begin{equation}
b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0
\end{equation}
であり、分子多項式は
\begin{equation}
a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0
\end{equation}
です。ここで、分母多項式を用いて
\begin{equation}
b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0=0
\end{equation}
を考えます。上式の根は個あり、それらを
と表記します。
には実数根だけでなく共役複素数となる根も含みます。同様に、分子多項式を用いて
\begin{equation}
a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 = 0
\end{equation}
を考えます。このとき、上式の根は個あり、それらを
とします。これも同様に共役複素数を含むことがあります。以上を踏まえ、
は次のように書き換えることもできます。
\begin{equation}
G(s) = \frac{a_m}{b_n}\frac{(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}
\end{equation}
システムの特性を考える上で上で示した表記は有用です。
をシステム
の極と呼びます。また、
をシステム
の零点と呼びます。特に、
の実部が
以上となる極を不安定極、
の実部が
以上となる零点を不安定零点と呼びます。
システムにおいて、
を次数といい、
と
の差を相対次数という。相対次数
が正の値のとき、
は厳密にプロパーといい、
が
のとき、すなわち
のとき双プロパーといいます。一般的な物理システムは厳密にプロパーもしくは双プロパーなシステムとして与えられます。
システムの伝達関数は、システムに対するインパルス応答のラプラス変換として捉えることもできます。
伝達関数の例1
システムの伝達関数がと与えられるとき、次数は
、相対次数は
、極は
であり、零点は
である。
は次のように書くことができます。
\begin{eqnarray}
G(s) = \frac{2(s+1+i)(s+1-i)}{(s+1)(s+2)(s+3)}
\end{eqnarray}

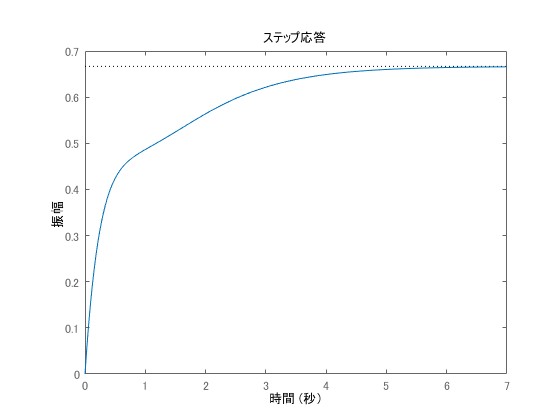
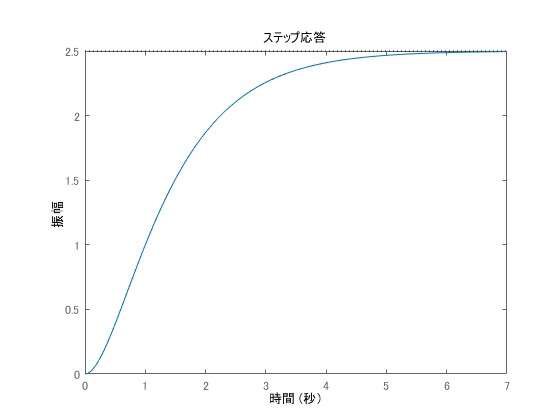
伝達関数の例2
システムの伝達関数がと与えられるとき、次数は
、相対次数は
、極は
です。
は次のように書くことができます。
\begin{eqnarray}
G(s) = \frac{5}{(s+1)(s+2)}
\end{eqnarray}
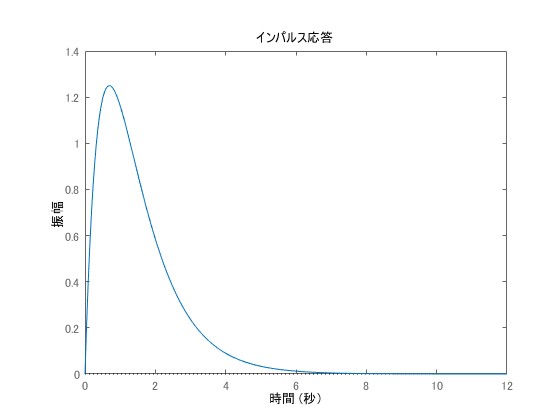
伝達関数の例3
システムの伝達関数がと与えられるとき、次数は
、相対次数は
、極は
(重根)であり、零点は
です。
は次のように書くことができます。
\begin{eqnarray}
G(s) = \frac{-s+2}{(s+1)^2}
\end{eqnarray}

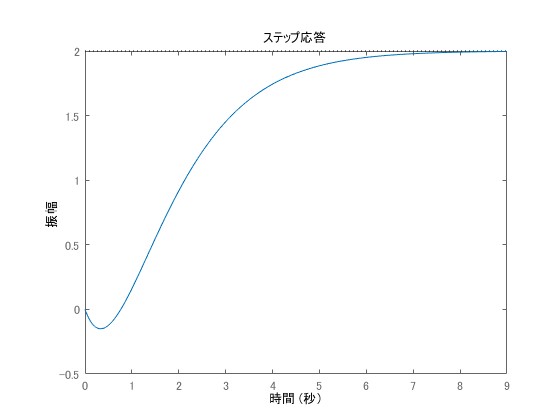
不安定ゼロ点が一つでもある場合、(安定な)逆モデルが作れません。
周波数領域での伝達関数の特性表現についてはボード線図がよく用いられます。関連記事はこちらです。
ラプラス変換・伝達関数の動画
以下は伝達関数について説明している動画になります。
予備校のノリで学ぶ大学の数学と物理のラプラス変換に関する動画です。
以上で説明を終わります。
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島寛 (システム制御 control-theory.com)
English Web Page
Hiroshi Okajima (Control Engineering control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。
以上がラプラス変換に関する記事になります。本記事は以上です。