この記事ではシステム同定・動的システムのモデリングについてまとめます。関連記事リンクや解説記事へのリンクは最下部に置いています。
システム同定の概要
それではモデリングシステム同定について説明をしていきたいと思います。まず制御工学において数式モデルは重要な役割を果たします。モデルベースの制御を行う場合には、まず制御対象の入出力特性に基づいてモデルを導出します。

そしてその得られた数理モデルに対して必要な性能が得られるような制御機器を設計するプロセスを踏みます。そのようにして得られた制御器を、実際に制御対象に適用することで制御を行うことになります。
このとき、モデルが精度良く求まっていれば、望ましい応答が、モデルに基づいて求めた制御器によって実現することができます。他方、精度の悪いモデルではよい制御の実現が困難になります。
モデル表現
ここでは制御対象の数式モデルの表現について説明したいと思います。制御でよく使われる方法としては、伝達関数および状態方程式というモデル化の表現が挙げられます。
また、時間を連続時間系として扱うか、離散時間系として扱うかという形でも分類がなされます。
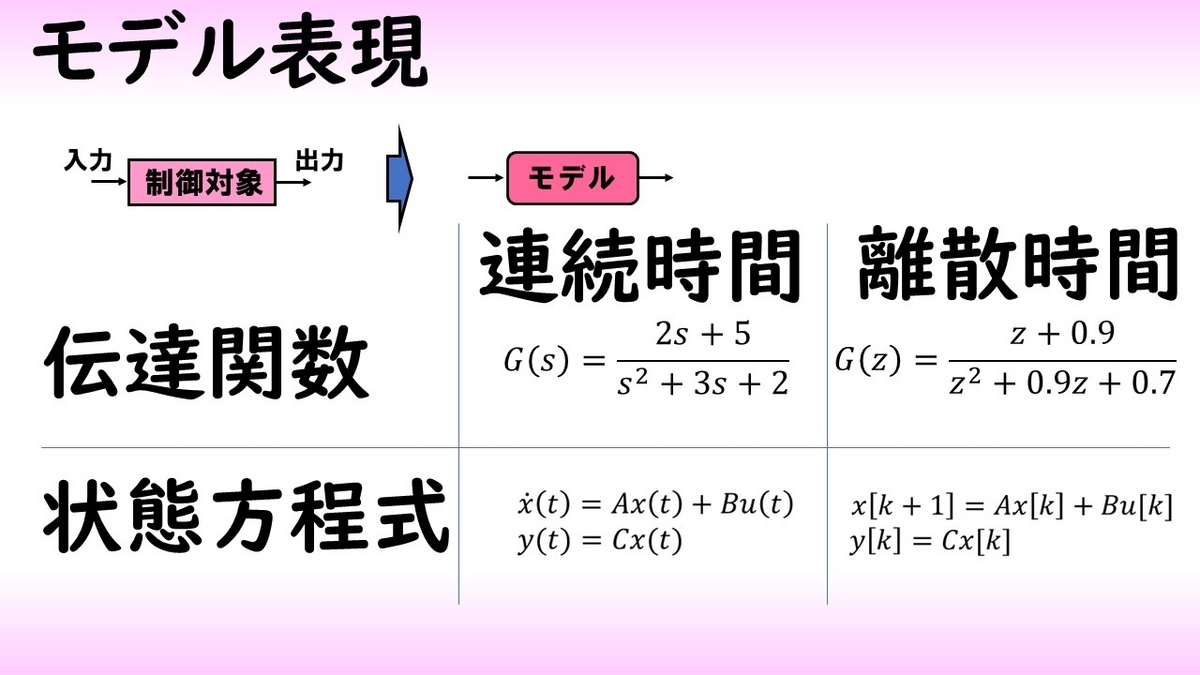
このように4つのモデル表現があるという前提のもとで、進めていきたいと思います。
ここではモデル化について説明します。数式モデルがあるとき入力から
までの特性が、対象の数理モデルになるように、それぞれの行列の値を決定することによって,モデルを得ることができます。具体的にはここでは
というそれぞれのパラメーターが適切に設定されることでこのようにプラントと同じ入力を印加したときに得られる出力が、数理モデルでも同じものになることが理想です。
適切な の行列が求まれば、数理モデルで対象と同じ入出力特性、入出力応答を実現できます。
ここでは2つのモデリングの方法について紹介します。
1つ目は制御対象 Pの物理法則。例えばバネ係数や回路の係数などから数理モデルを求めるというものです。2つ目の方法として数理モデルの中身パラメータや物理法則などがわからないものとして、入力uと出力yのデータから数理モデルを求める、という方法があります。
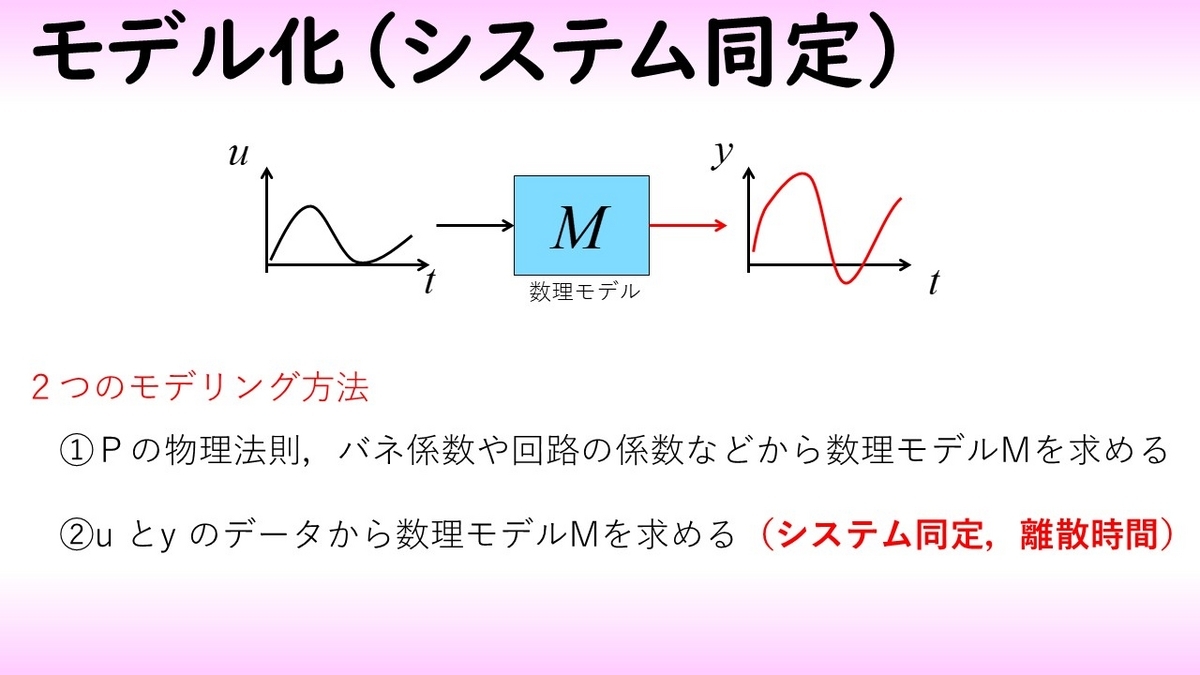
これはシステム同定と呼ばれる方法であり、この後で説明する方法になります。
ここでシステム同定を扱うときには、基本的には離散時間のパラメータが求まることに
なります。
しかしながら離散時間での伝達関数や状態方程式が求まったとき、それに基づいて連続時間の状態方程式や伝達関数に変換することができますのでこのような相互変換が可能という中で、システム同定で離散時間モデルを求め、もし連続時間モデルに変換する必要があれば、連続時間モデルに変換する、というプロセスでどのモデルも求まることになります。
実際にそのモデルを得た上での、制御系設計や実装のプロセスにおいては、制御対象の
モデル、不確かさの大きさ、外乱の性質や制御系の実装における観測出力、操作入力などさまざまな要素が必要になりますがこのモデルをうまく構成することによって、
制御をより精密に行うことができるといえます。
一般にシステム同定ではシステムを表現するためのモデルの構造が先に与えられます。
ここで、入力が、出力が
として与えられています。
に含まれる
はシステムのパラメータになります。
それでは実際にシステム同定の手順にいきたいと思います。プロセスは簡単です。
まず入力と出力
のデータを取得します。この入力
と
のデータを取得する際に、入力
は PE性と呼ばれる情報の律さを示す指標をうまく満たすように決める必要があります。
そして得られた入出力データに対して同定アルゴリズムを使ってパラメータを決定します。
代表的なものとしては、部分空間同定法や予測誤差法などが挙げられます。
以降ではMATLABを用いたシミュレーションを行っていきます。
システム同定のシミュレーション例
MATLABではこの部分空間同定法や予測誤差法は、関数として与えられていますので、それを使って同定を行ってみます。
それでは実際に MATLAB でシステム同定を行っていきたいと思います。
まず制御対象としてはこちらの制御対象を考えます。そしてこれに対してチャープ信号と呼ばれる信号を印加して、その結果システム同定を行います。
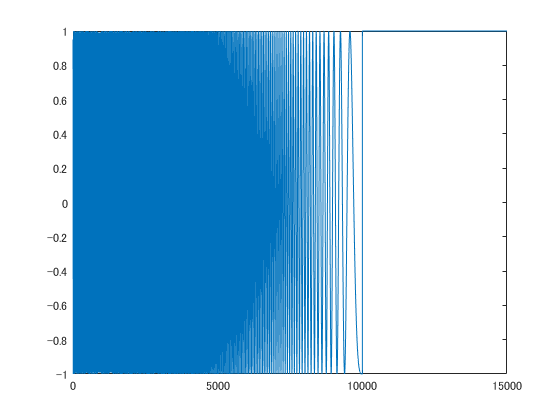
ここではまず入力としてチャープ信号を生成し、それを用いて入出力データを求めます。
出力データはこちらで与えられます。ここでノイズも含むような系となっていることに注意してください。ノイズが含まれている環境下でしっかり同定できていることを、この数値例では確認したいと思います。
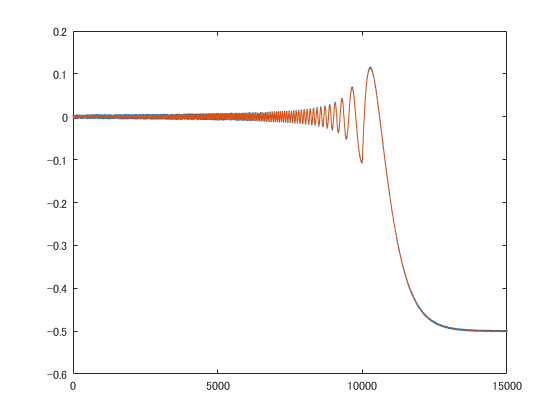
こちらがチャープ信号と呼ばれる信号を印加した時の出力であり、様々な周波数成分を持った入力に対して、出力がこのように得られています。
こちらが元のシステムと同定により得られたシステムの、それぞれのステップ応答になります。青が元のシステム、オレンジがモデル出力です。
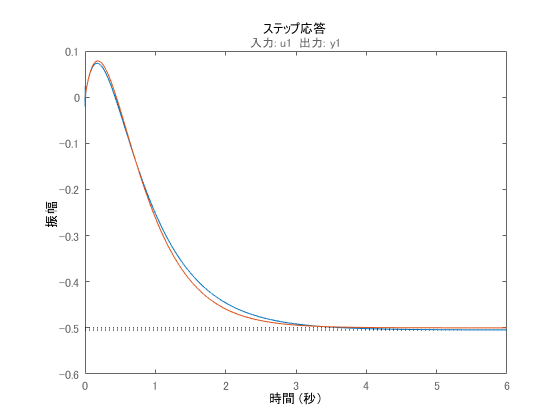
波形が似通っていることが分かりますがその一方で誤差があります。この誤差が大きくなるか少なくなるかはシステム同定における様々な設定に依存して決まってきます。
こちらが制御対象と同定によって得られたシステムのボード線図になります。低周波ではほとんど一致していることが分かるかと思います。
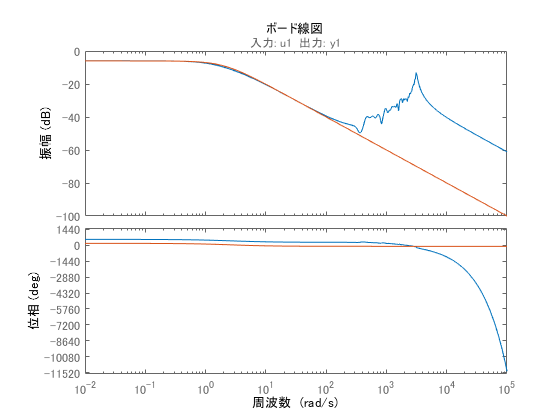
数理モデルの相互変換について
連続時間,離散時間のそれぞれは相互に変換でき,また,伝達関数と状態方程式も変換できます。何等かの手法でモデル化後に実際に利用したいモデルに変換を行い,適用範囲の中で設計していくことが重要になります。

システム同定の動画・関連記事
以下はシステム同定・モデリングについて説明している動画になります。
大阪工業大学の奥先生の動画です。
システム同定の書籍
システム同定に関する書籍をいくつかピックアップします。
足立先生の書籍はこちらです。
北九州市立大の藤本先生と広島大の永原先生のシステム同定の本がこちらです。
和田先生、奥先生、田中先生、大松先生のシステム同定の本がこちらです。
片山先生のシステム同定の本がこちらです。
本記事は以上です。
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。




