ボード線図 - 制御工学ブログ

この記事ではボード線図についてまとめます。ボード線図について説明した動画や関連記事リンクは最下部に置いています。まず、安定な伝達関数が与えられたものとし、その特徴を周波数領域で表現する方法としてボード線図が良く用いられます。

関連記事として以下のラプラス変換の記事を併せてご覧ください。

対象システムの伝達関数表現

対象システムの伝達関数表現

ここでは、システム $G$ の伝達関数を $G(s)$ と表記し、その伝達関数固有の性質について考えます。

\begin{equation}
G(s) = \frac{a_{m} s^{m} + a_{{m}-1} s^{{m}-1}\cdots + a_1s + a_0 }{b_n s^n + b_{n-1} s^{n-1}\cdots + b_1s + b_0}
\end{equation}

ここで、 $n, m$ は自然数であり、分子および分母は $s$ に関する多項式です。各多項式における係数 $a_0, \cdots, a_m$ および $b_0,\cdots,b_m$ は実数で与えられます。ここでは、システム $G$ の極 $p_1,p_2,\cdots,p_n$ は安定極であることを仮定して話を進めます。

安定なシステム $G(s)$ に入力信号として正弦波 $u(t) = \sin (\omega t)$ を印加する場合を考えます。ここで、 $\omega$ の値が大きいと速い正弦波になりますし、 $\omega$ の値が小さいと遅い正弦波になります。そして、システムが安定な場合には、定常状態で出力にも同じ角周波数 $\omega$ の信号が現れることになります。

ボード線図の表現

どんな入力を印加すると、どんな出力が得られるかを考えます。伝達関数 $G(s)$ の $s$ に $s = j\omega$ を代入してその大きさと角度を計算すれば、ある角周波数 $\omega$ を印加したときの出力 $y(t)$ が次のように特徴づけられます。

\begin{equation}
y(t) = |G(j\omega)| \sin (\omega t + \angle G(j\omega) )
\end{equation}

ただし、上式は、制御対象が安定の前提下で、時間の経過とともに過渡的な信号が減少した後の最終的な定常出力を表している点に注意してください。

このとき、出力信号の振幅の大きさが $|G(j\omega)|$ で特徴付けられ、位相の遅れが $\angle G(j\omega)$ で特徴付けられます。

このことは、安定な伝達関数にサイン波を入力した上で部分分数分解した場合、安定項に対する応答は時間の経過とともに零となり、サイン波に対応した応答のみ残ることから理解することもできます。

blog.control-theory.com

ここで、出力について、入力振幅が二倍になれば出力振幅も当然二倍になりますが、ここでボード線図では、振幅比を表現することから入力の大きさは考えず、入出力比を表現するために $|G(j\omega)|$ で特徴付けられます。ボード線図は横軸を角周波数 $\omega$ として、ゲインと位相を表したものであり、伝達関数 $G(s)$ さえ与えられれば、そこから容易に計算できます。通常、ゲインはデシベル表記するため $20 \log_{10} |G(j\omega)|$ で与えられます。

ボード線図の例

システムの伝達関数が $G(s) = \frac{1}{(s+1)(s+2)}$ で与えられる場合について、そのボード線図を示します。

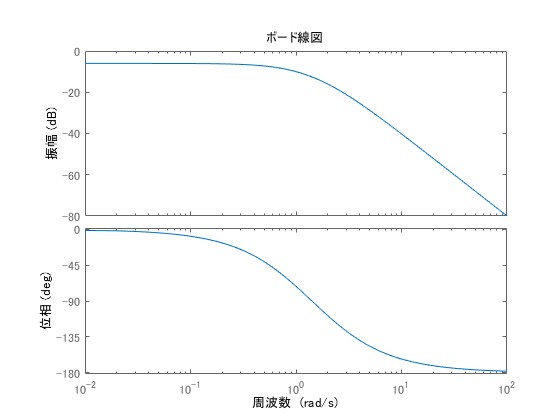
インナー要素のボード線図

インナー関数のボード線図を示します。以下の $G_1(s)$ を考えます。

\begin{equation}
G_1(s) =\prod_{i=1}^N \frac{(s-\bar z_i)}{(s+z_i)}
\end{equation}

ここで、安定であるためには、 $z_i$ は全て安定極であるものとします。当然、零点は不安定になります。ここでは、例として $N = 2$ とし、 $z_1 = 1, z_2 = 2$ の場合のボード線図を示します。

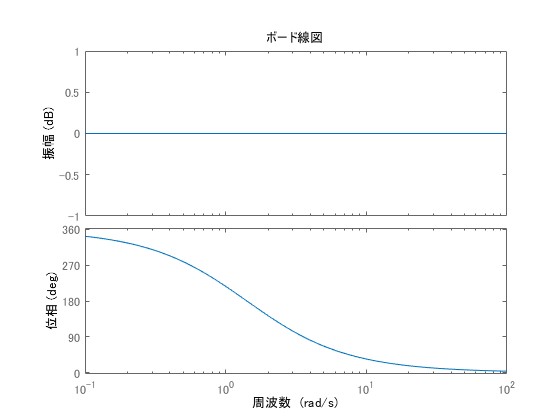
このとき、全ての周波数でゲインが $0 dB$ すなわち、 $1$ 倍であることがわかります。他方、位相は大きく変化しています。インナー関数を使うと、ゲイン特性が同じで位相特性が異なる伝達関数を作成することができます。ここで、対象システムが不安定零点を持たないとき、同じゲイン線図となる伝達関数のうち位相が最小となることから、不安定零点を含まない最小位相系とも呼ばれます。不安定零点を含むシステムは制御が格段に難しくなることが多いです。