本記事では、不安定零点を持つシステムの制御方法について述べます。以下の文献の簡易版です。より詳細について内容を知るためには,以下のリンクからご覧ください。
不安定零点
以下が、不安定零点を持つ制御対象伝達関数の一例です。
![]()
伝達関数において、零点は分子多項式 = 0 を満たす s であり、一つ目の対象の零点は s = 1 であり、二つ目の対象の零点は s = 1 ± i です。双方ともに実部が正の値を取っています。零点の中で一つでも不安定零点を持つと制御が極端に難しくなります。
不安定零点を持つシステムの実例
制御系を設計では,多くの場合において制御系の極に注目します。しかし,適当な減衰率となるように制御系の極を配置したとしても時間応答が期待通りの波形にならない場合があります。これには制御対象の零点が関係していて,制御対象の零点がフィードバック制御によって実現できる潜在的な能力や限界を表していると言っても過言ではありません。特に制御対象が不安定零点を持つ場合には,制御系の設計において良い応答を実現することが困難なことが多いです。
不安定零点はロケットや飛行機,センサとアクチュエータが非コロケーションになりやすいプロセス制御系などでよく生じます。また,制御の困難さから不安定極・不安定零点を持つ倒立振子は古くから制御の題材としてよく用いられてきました。
不安定零点を持つシステムの表現
制御対象が不安定零点をN個もつ場合、以下の表現が見通しが良いです。
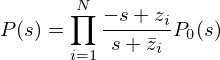
z_iを不安定零点とし、P_0 は、安定かつ最小位相の伝達関数とします。
逆システムについて
不安定零点を持つ対象は、逆システムが不安定になります。具体的に、上記のP(s)において、不安定零点の逆数を取ると不安定極になるため、不安定零点を持つ対象の逆システムを構成することはできず、近似的な取り扱いをします。具体的には、上記のP(s)においてP_0(s)の逆システムを掛けた系を考えると低域では逆システムとして機能することになります。
逆応答
不安定零点を持つシステムで生じる現象の一つに逆応答があります。応答波形の例は以下になります。

これは、ステップ信号を印加したものであり、最終的に出力信号が1に収束しています。一方、時刻 0 秒付近では、一旦収束値とは逆向き(下向き)に動いてからプラスの値に向かっています。このような応答を逆応答(逆ブレ)といいます。
不安定零点を持つ対象では、逆ブレが生じます。特に、1個の不安定零点を持つ場合は時刻 0 から収束値と逆方向に行くことが知られています。不安定零点の個数で初期の振動が変わってきます。この辺りの説明は以下の文献が詳しいです。
制御性能限界
不安定零点を持つ制御対象では、制御性能に限界があります。具体的には、目標値追従制御を行う場合に、追従偏差の値は 0 が理想です。常に追従偏差が 0 となるような制御をパーフェクトトラッキングと呼びます。このような制御は最小位相系では実現できますが、不安定零点を持つと実現不可能です。どのような制御性能なら実現できるかは、零点の値に依存してきます。例えば以下の文献において、追従誤差(追従偏差)の2ノルムの下限が見積もられています。
>>あるクラスの参照信号に対する追従性能限界の解析 (jst.go.jp)
この他、以下の文献内では、並列フィードフォワード補償器や、非線形系における零ダイナミクスとの関係などについて解説をしています。
本記事は以上になります。本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト