この記事では状態方程式表現されたシステムの状態フィードバック制御についてまとめます。状態方程式表現されたシステムの最適レギュレータについて説明した動画を最下部に置いています。
なお、状態フィードバック制御の全体像は次の記事でまとめています。
最適レギュレータの状態フィードバック制御構造
それでは状態フィードバックと最適制御、最適レギュレーターついて説明をしていきます。最適レギュレータは制御工学分野で広く知られた基礎的な設計手法の一つです。
まず状態フィードバックについての説明をします。状態方程式表現をされた制御対象は以下のように与えられます。
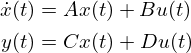
制御入力がu、制御出力がyとなります。多くのケースではD=0となります。状態はxです。状態フィードバックでは
![]()
と、状態に係数をかけたものを入力として用います。ここで、良く用いられるK, Fを例として記号化していますが、どんな記号を用いるかは論文により様々です。また、記号の前に陽にマイナスをつけるケースもあります。制御対象の状態量の例としては、速度や位置などが挙げられますが、詳しくは状態方程式の説明をご覧下さい。

ここでは状態フィードバックゲインを決める方法としての最適レギュレーターについての説明をしていきます。
まず状態方程式中の主な記号は以下のようになります。まず t が時間であり x が状態ベクトル、uが入力 、y が出力です。nが次数であり、状態のベクトルの要素数に対応します。 Aはn次の正方行列で、Bは n次の縦ベクトル、Cは n次 の横ベクトルとなります。これはただし、入力と出力の数が1個のケースが図のようになります 。

次の制御則
![]()
を施したとき、その制御系(自律系)は次のように与えられます。
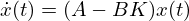
最適レギュレータの考え方
次に、最適レギュレーター問題でどういうことを考えていくかについて説明します。

最適レギュレーター問題では、まず次のような評価関数を考えます。
![]()
この評価関数は状態 xにQをかけた二次形式のものになっており、それと Ru に関する二次形式の項の線形和で表されています。評価区間は時刻 t = 0 から時刻無限大までとなっています。無限区間の評価区間です。
この評価関数値Jを最小にするようなゲインKを求める問題のことを最適レギュレーター問題と呼びます。ここで評価区間は時刻0秒を基準として無限大までとっていますが、ここは便宜上ゼロとしているだけで別の時刻からスタートしても構いません。
この二次形式の係数行列Qと Rは、重み行列と呼ばれるもので x を重視する場合にはQを大きめに取る、入力uを重視する場合は Rを大きく取るといった扱いがなされます。第一項が小さければ小さいほど、x が早くゼロに収束するような解が良いことを意味しており、他方、第二項が小さいほど入力エネルギーが小さくて済む、ような解が良いということを意味しています。
そして最適レギュレーター問題では、この収束の速さとエネルギーの少なさを両立する
制御手法といえます。

最適レギュレータ問題の解
ここで最適レギュレーター問題の解を先に説明します。この最適レギュレーター問題の解は、すでに求められており以下のようなステップで求めることができます。

まずは図のステップ 1 で示すように、リカッチ方程式(リッカチ方程式, Liccati方程式)と呼ばれるこのこちらの方程式を満足する正定行列 Pを求めます。これが最初のステップです。
この解は、代数計算として求めることができます。
そして、ステップ 2 でこの得られた正解 Pを使って、ゲインを Rの逆行列かけるBの転置かけるPというふうに設定してやると、それが先ほどの最適レギュレーター問題に対する最適解になります。
最適性の証明については、後半にある動画をご覧ください。
数値例を用いた最適レギュレータの検証
MATLAB でゲインKを求めるときには、この lqr という関数を使って、リカッチ方程式を解いてゲインKを求めることができます。
ここでは n =3、次数が3次のシステムの最適レギュレーターの設計の例を考えていきます。

制御対象がこのように与えられていて状態ベクトルは要素が3つあります。重み行列の要素を単位行列として与えてRの重みを0.01とした場合を最初にシミュレーションします。
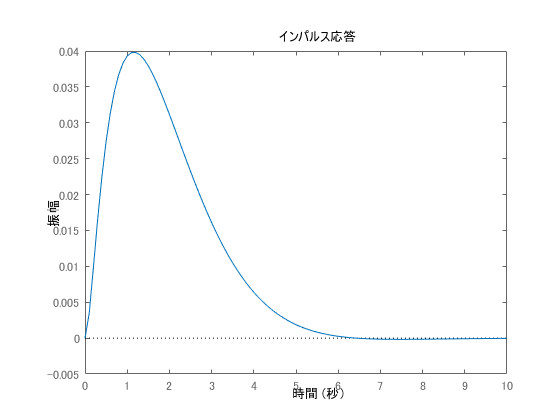
その後で入力を重視してより省エネを目指すような評価値を、評価関数を考えたケースを2番目にシミュレーションしていきます。R = 1 および R = 100 を示します。
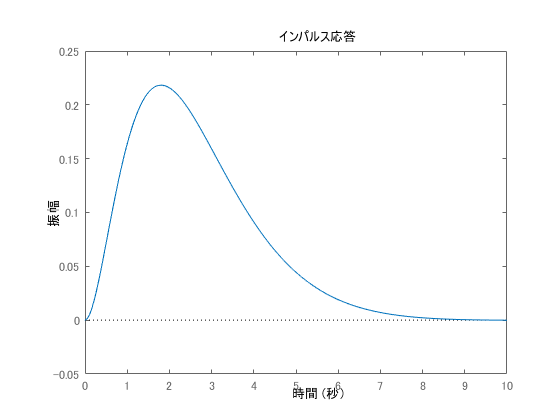
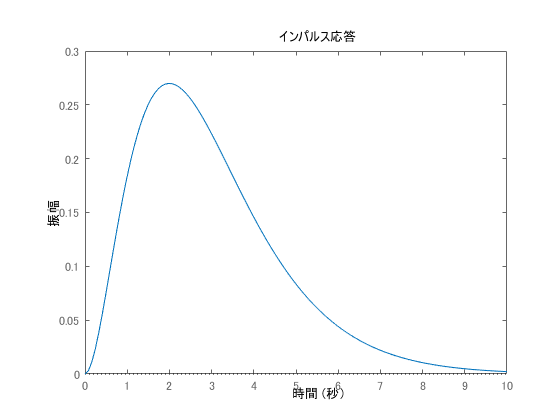
Rが大きいほど、振幅が大きくなることが許容された制御結果となっていることがわかります。入力については波形を示していませんが、u = K x の時間推移を示した場合、逆に u はRの重みが大きい方が小さな値(時系列)となります。
その他のMATLABシミュレーションについては次の記事をご覧ください。
以上が最適レギュレーターに関する説明になります。
関連動画
以下は,状態方程式表現されたシステムの最適レギュレータについて説明した動画になります。
MATLABシミュレーションによる最適レギュレータ
関連ページ(最適制御)
>>制御工学チャンネル:500本以上の制御動画ポータルサイト Control Engineering Channel - 01-Prof.Okajima-02 (control-theory.com)
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。