状態オブザーバとは？基本メカニズムを理解する

この記事では状態方程式表現されたシステムの状態推定器（状態オブザーバ）についてまとめます。状態方程式表現されたシステムの状態オブザーバについて説明した動画は最下部に置いています。オブザーバは，観測できない情報を計算機内で観測することからソフトウェアセンサー（ソフトセンサ）とも呼びます。

なお、状態フィードバック制御の全体像は次の記事でまとめています。

状態フィードバック制御・状態方程式に基づく制御のまとめ

状態オブザーバの概要
状態オブザーバの基本的な考え方
- オブザーバの立式
状態オブザーバのシミュレーション
オブザーバ併合系
状態オブザーバが必要となる具体的な場面
オブザーバ設計の実践的手順と注意点
状態推定に関する関連動画
状態オブザーバの研究
制御工学チャンネル内の関連ページ（状態オブザーバ）
- 自己紹介

状態オブザーバの概要

それでは状態オブザーバーについて説明をしていきたいと思います。制御系において、必ずしも、システムのすべての信号をセンシングできるとは限らないことから、状態を推定する必要があります。状態方程式において、一般的に（速度や位置など）の変数を状態とし、観測出力とは別のものとして考えます。状態の値を用いた状態フィードバックを施す上ではわからない状態を推定する必要があります。例えば状態が[位置],[速度]の2つで、観測出力が[位置]のみの場合は[速度]は計測されていないため、速度推定値を求める必要があります。

制御対象が図のように与えられていて、これにu=-Kx という状態フィードバック制御を施す場合を考えます。状態フィードバック制御は制御工学分野で最も基礎的な制御手法の一つです。このとき、状態フィードバック制御では、すべての状態を使うことが前提となっています。状態オブザーバによって推定値が求まれば、その推定値を代わりに用いることで状態フィードバック制御が実現できます。

状態量と状態フィードバック制御の関係について示す図 — 状態フィードバック制御と状態量

一般的には、状態の数と観測できる出力の間には、図のような関係があり、状態数の方が、観測できる出力数よりも多くなります。

センサと状態の信号数が異なること、センサが少ないことを示した図 — センサ数と状態数の関係

状態オブザーバの基本的な考え方

ここでオブザーバーの基本的な考え方について説明します。

まず制御対象のダイナミクスが以下の図の上部ように与えられていたとき、これに対して同じA, B, C 行列で与えられる、制御対象のコピーを計算機上に作成します。これを数理モデルと呼びます。制御対象に制御入力を印加したとき、それに対して出力が現れますが、制御対象と同じ入力を制御対象のコピーに印加してやると、数理モデルの状態は制御対象の状態に似た振る舞いをします。

仮に、システムのA行列の極が安定極の場合、さらに、制御対象の状態と数理モデルの状態の初期値が一致していれば、外乱なし環境下では制御対象の状態と数理モデルの状態とが全ての時刻で完全に一致します。

状態の初期値が一致していなくても、Aが安定な場合に関しては、この初期値の影響は時間の経過とともに小さくなっていきますので、入力を入れてしばらくすると制御対象の状態と制御対象のコピーである数理モデルの状態とが近くなっていきます。

このため、数理モデルの状態を制御対象の状態とみなして状態フィードバック制御で用いることができます。

ここでさらに、この制御対象の出力と、この制御対象のコピーにおける出力との偏差をフィードバックに用いることによってより収束の精度を良くすることができます（下図参照）。

以上がオブザーバーの考え方になります。

オブザーバの立式

具体的に基本となる状態オブザーバーは以下の式で与えられます。

$\dot {\tilde x} (t) = A\tilde x (t) + B u(t) - L(C\tilde x(t) - y(t))$

ここで、 $y(t)$ は観測出力です。

このような構成を行うことによって、 $\dot x(t) = Ax(t)+Bu(t)$ との差を考え、状態の推定誤差 $e(t) = x(t) -\tilde x(t)$ に関するダイナミクスは次式で示されるダイナミクスとなります。

$\dot e(t) = (A-LC) e(t)$

ここで $A - LC$ の項が安定となるようにLを設定してやると、それによってeはゼロに漸近していきます。このオブザーバは $A$ が不安定であっても $(C,A)$ の組が可観測であれば実装可能です。

状態オブザーバーの仕組みであり、これによって状態と、状態の推定値との偏差がゼロとなることから、状態の推定値を状態だとみなして制御に用いることによって、制御系全体がうまくいきます。

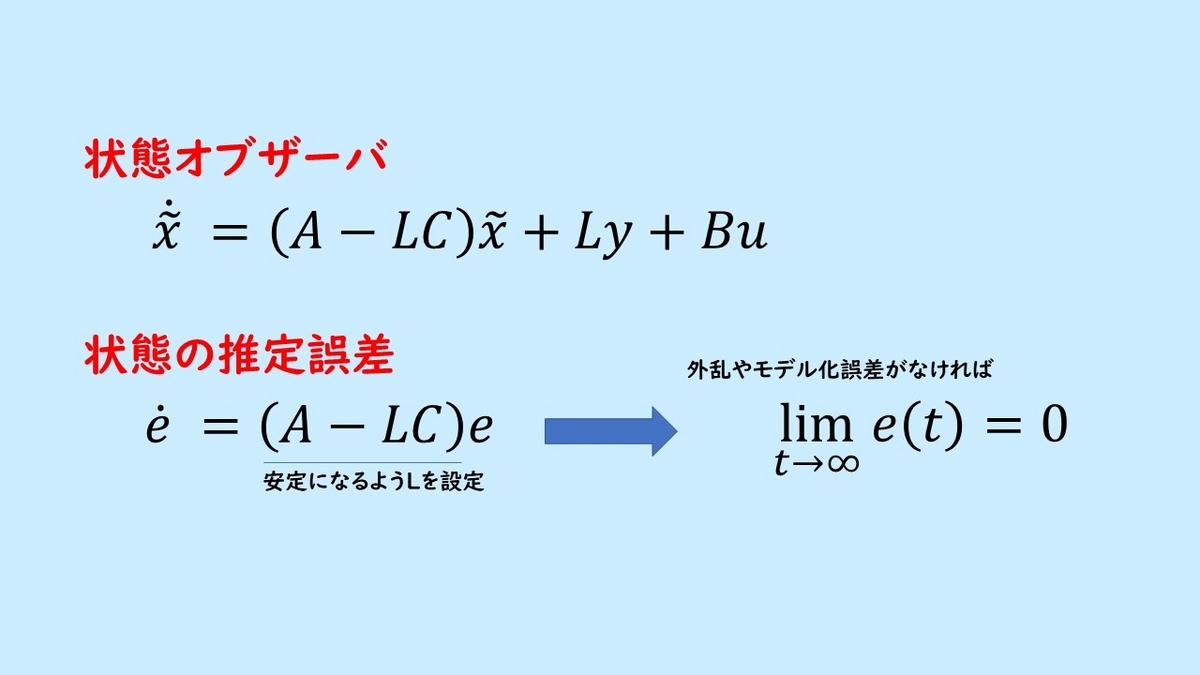
以下が制御系の状態方程式表現におけるオブザーバのまとめスライドになります。

ここまで、状態オブザーバの基本構成と立式について説明を行いました。以上で状態オブザーバの説明を終わります。

状態オブザーバのシミュレーション

制御対象は次のように与えられるものとします。状態数2とし、一入出力とします。

\begin{equation} \dot x(t) = Ax(t) + B u(t) \end{equation}

\begin{equation} y(t) = Cx(t) \end{equation}

出力が1個であるのに対して、状態数は2あるので、そのままでは状態フィードバック制御ができません。これに対してオブザーバを用いて状態を推定します。

初期値を $x(0) = [1, 2$ ]とし、入力は $u(t) = \sin(t)$ として印加します。出力信号は次のように与えられます。

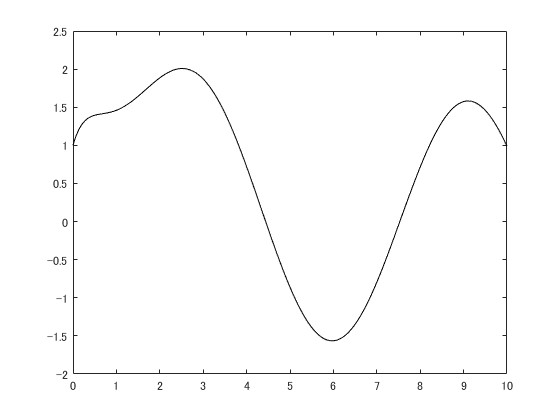
状態オブザーバの初期値は $\tilde x(0) = [0, 0$ ]とします。２つの状態軌道は黒色で与えます。赤は推定値です。

制御対象の初期値と状態推定値の初期値の差が最初に現れていますが、それが時間の経過と共に現象していき、時間が経過すれば推定誤差が零になります。

次に、オブザーバゲインを変更した場合の応答を示します。 $A - LC$ の極を左に配置した場合の応答を示します。スケールは異なりますが、黒は全く同じ波形です。赤の状態推定値がオブザーバゲインの変更に従って変わっています。極を左に配置してオブザーバを設計したため、状態推定値が制御対象の状態に速く収束します。

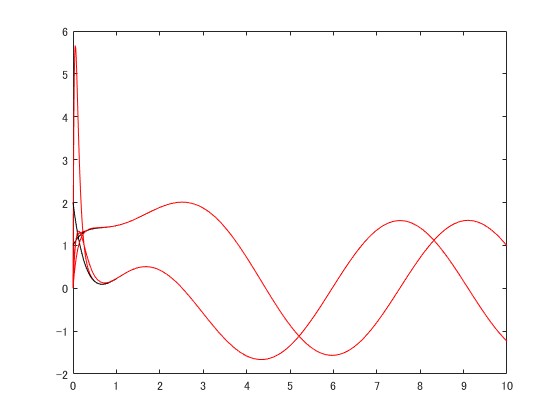
なお、仮に制御対象の初期値を知っている場合、オブザーバの初期値も制御対象の初期値と一致させてオブザーバを走らせることになります。そのような場合、初期値以降の全ての時刻で制御対象の状態と状態オブザーバの状態（状態推定値）とが一致します。その様子は以下の通りです。赤と黒の線が完全に重なっています。

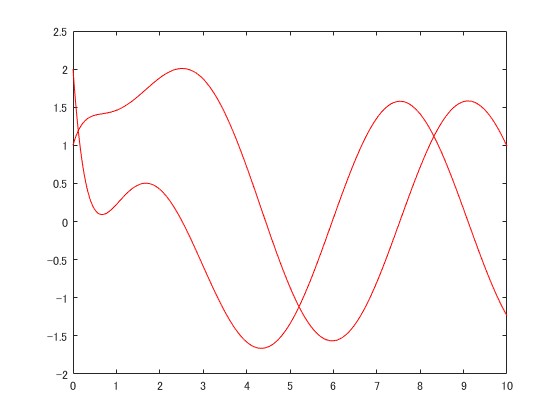
制御対象の初期値と状態オブザーバの初期値が一致している場合の応答（赤と黒が完全一致）

入力を矩形波にした場合が以下のようになります。

オブザーバ併合系

状態オブザーバと状態フィードバックを併用したシステムをオブザーバ併合系（オブザーバ併合状態フィードバック制御）と呼びます。

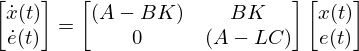
オブザーバ併合系

システムの次数は $2n$ となり、オブザーバ構成によって得られる閉ループ極（ $A-LC$ の極）と、状態フィードバックによる閉ループ極（ $A-BK$ の極）とが制御系の特性を決めることになります。このように、それぞれオブザーバと制御器を独立に設定できる特徴のことを分離原理と呼びます。

オブザーバ併合系での制御入力は $u = -Kx$ の代わりに推定値 $\tilde x$ を用いて $u = -K\tilde x$ とします。そのため、状態偏差 $e(t)$ は速く収束してほしいので、オブザーバ極は複素平面上のより左側に配置することになります。

blog.control-theory.com

状態オブザーバが必要となる具体的な場面

状態オブザーバが必要になるのは、測定したい状態変数を直接センサで取得できない場合です。最も代表的な例がモータ制御です。DCモータでは回転角度はエンコーダで測定できますが、角速度センサは高価でノイズも多いため、位置情報から速度を推定するオブザーバがよく用いられます。

また、自動車のエンジン制御では、燃焼室内の空燃比は直接測定が困難なため、排気ガス中の酸素濃度から推定します。バッテリ管理システムでは、充電状態（SOC）や劣化度（SOH）といった内部状態は直接測定できないため、電圧・電流・温度の測定値から推定する必要があります。これらの場面で状態オブザーバはコスト削減と信頼性向上を同時に実現する重要な技術となっています。

オブザーバ設計の実践的手順と注意点

状態オブザーバの設計では、まずシステムの可観測性を確認することが必須です。可観測性行列のランクチェックにより、選択したセンサ配置で全ての状態が推定可能かを判定します。次に、併合系で説明したように、極配置法では推定誤差の収束速度を制御対象の極より3～5倍速く設定するのが一般的です。速すぎると測定ノイズを増幅し、遅すぎると制御性能が劣化します。

実装時の重要な注意点として、初期値設定があります。オブザーバの初期推定値が実際の状態と大きく異なると、推定が収束するまで制御性能が悪化します。また、モデル誤差に対する対策も必要で、実際のシステムと設計に用いたモデルが異なる場合、推定精度が劣化します。この対策として適応オブザーバやロバストオブザーバの手法があり、実用システムでは不可欠な技術となっています。