外れ値にロバストな状態オブザーバの構成：複数の候補とメディアンを利用した状態推定アプローチ

本ブログでは、外れ値がセンサ信号に含まれる系での状態推定について説明します。まず、外れ値を含む系の状態推定問題を定式化します。ここでは、外れ値の問題に対処するために複数の候補を並列に定め、その中から外れ値の影響を受けていない推定値を選択する新たな状態推定法を提案しています。

[link] H. Okajima, Y. Kaneda and N. Matsunaga: Full article: State estimation method using median of multiple candidates for observation signals including outliers (tandfonline.com) SICE JCMSI (2021)

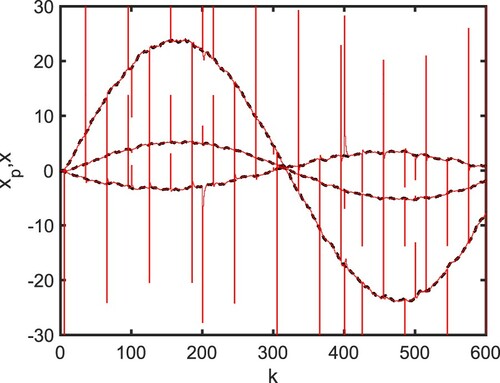
本論文は、松永先生、金田さんとの共著です。以下の図は、センサ信号（観測出力信号）に外れ値が含まれる例を示しています。

Sensor output with outliers — Sensor outputs with outliers

通常の状態推定器を用いた場合、外れ値の影響で推定精度がかなり悪くなります (Figure 2)。その一方、提案法を用いることで、かなり良い推定精度での状態推定が可能になります(Figure 3)。以降では、そのメカニズムについて説明していきます。

Figure 2: Estimated state by traditional observer

Figure 3: Estimated state by proposed observer (MCV observer)

問題設定
MCVオブザーバ
メディアン操作とは？
リンク [Full Paper, MATLAB codes]

問題設定

本研究では、離散時間線形時不変システムを対象としています。現在時刻を $k$ とし、制御対象の動特性は以下の状態方程式で与えられるものとします。

$x_p(k+1) = A x_p(k)+B_u u(k) +B_d d(k)$
$y(k) = Cx_p(k)+Dw(k)+y_{out}(k)$

行列 $A$ 、 $B_u$ 、 $B_d$ 、 $C$ 、 $D$ は、制御対象の動特性を表す正方行列と入出力に対応する行列であり、制御対象の次数は $n$ とします。

$y_{out}(k)$ は外れ値を表します。通常時は $y_{out}(k) = 0$ が成り立ちますが、 $k = k_1$ で外れ値が発生した場合、 $y_{out}(k_1) \neq 0$ が成立します。この、 $|y_{out}(k_1)|$ の大きさに制限はありません。外れ値はノイズよりも劇的に大きいと考えられます。

特に、 $y_{out}(k) = 0, \forall k$ が成立する場合は、外れ値のない観測出力を意味します。また、 $y_{out}(k) = -Cx_p(k)-Dw(k)$ が成立する場合、 $y(k)=0$ のようなパケット損失を表現することができます。観測値やノイズから外れ値を区別するために、ここでは $y_{out}(k)$ の絶対値が他の信号と比較して十分に大きいと仮定します。

外れ値 $y_{out}(k)$ の詳細な定式化を示します。本研究では、外れ値は瞬時に発生するものとします。言い換えれば、外れ値は短期間に発生すると考えています。2つの整数 $F_1$ と $F_2$ は、観測された出力における外れ値を特徴付けるために用いられています。任意の時間間隔[tex： $k$ の時間間隔[k, \cdots, F_1-1]において、その時間間隔に現れる外れ値の最大数は $F_2$ であるものと仮定します。これを言い換えれば、 $F_1$ は時間区間を決定し、 $F_2$ は時間区間における外れ値の出現頻度を特徴付けています。

MCVオブザーバ

本研究では、 $F_1$ と $F_2$ について、以下の条件を満たすと仮定します。

$F_1 \geq 2F_2 + 1.$

外れ値はセンサー出力の様々な設定においてまばらに発生することが多いです。このような場合、前述の仮定は容易に満たすことができます。

状態推定値の候補

まず、状態推定値の候補について述べます。MCVオブザーバ（提案する状態オブザーバ）では、時刻 $k - i$ の推定値を用いて時刻 $k + 1$ の状態を推定するものとします。ここで、過去に推定した状態 $x (k-i)$ を用いた推定値を $\hat x_i (k + 1)$ と表記します。

$\hat x_i(k+1) = (A^{i+1} - L_i C) x(k-i) \\+ L_i y(k-i) + \sum_{j = 0}^i A^j B_u u(k-j)$

ここで、 $\hat x_i (k + 1)$ は時刻 $k + 1$ における状態の推定値（の候補）を表し、各 $i$ について推定値の導出では $y (k-i)$ の値のみが観測出力として使用されています。 $L_i$ は $\hat x_i(k+1)$ を得るためのオブザーバゲインです。他の時刻の観測出力（ $k-j,jneq i$ ）は使用しないことに注意が必要です（本手法の特筆すべきアイディアです）。

外れ値の判定

外れ値の影響を受けた推定値候補の除去のために以下の出力 $y_e(i)$ を定義します。

$y_e(i) = y(k-i) - CA x(k-i-1) - CB_u u(k-i-1),$

ここで、 $x(k-i-1)$ と $u(k-i-1)$ は既知の値であり、 $y(k-i)$ は観測された出力であるため、各々の $i$ について $y_e(i)$ を計算することが可能です。別の表現として、信号 $y_e(i)$ は以下のように表すことができる。

$y_e(i) = CA e(k-i-1) + Dw(k-i) \\+ CB_d d(k-i-1) + y_{out}(k-i),$

ここで $e$ は $x_p(k)$ と $x(k)$ の誤差であり、すなわち、 $e(k) = x_p(k) - x(k)$ が成り立ちます。外れ値が発生した場合、 $y_{out}(k-i)$ の影響力は、 $y_{out}(k-i-1)$ 、 $w(k-i)$ 、 $d(k-i-1)$ の影響力よりも非常に大きくなります。この性質を利用して $y_e(i)$ を外れ値が含まれるか否かの判定に利用します。

MCVオブザーバのアルゴリズム

MCVオブザーバは以上のコンセプトに基づいて次のようにアルゴリズムが記述されます。

オブザーバゲインの設計

オブザーバゲインの設計については、論文内をご覧ください。不変集合解析に基づいた設計論を展開しています。

メディアン操作とは？

中央値演算（メディアン操作）は、多くのコンピュータ装置において計算コストが小さいため、幅広い研究分野で利用することができます。例えば、画像処理におけるフィルタとして利用され、原画像からゴマ状ノイズを除去するのに有効であることが知られています。

中央値とは、データを大きさの順に並べた場合に、データ全体の中心に位置する値のことです。数値の数が偶数の場合は、中心に位置する2つの数値の平均値をとることで求めることができます。値を昇順に並べたときのデータ $\xi (i), i = 1, \cdots, n$ は $\tilde \xi{(1)}, \tilde \xi{(2)}, \cdots, \tilde x{(n)}$ となります。中央値 ${\xi}_{m}$ は以下のように求められます。