RLC回路の過渡現象解析

この記事ではRLC回路の過渡現象についてまとめます。本記事の元となった関連動画は最下部に置いていますので、理解のためにそちらもご覧ください。

微分方程式について
RLC回路の過渡現象について
[動画]RC回路の過渡現象
[動画]RLC回路の過渡現象
- 自己紹介

微分方程式について

以下は，過渡現象について説明した動画になります。

youtu.be

また、以下は、微分方程式の解法について説明した動画になります。RC回路の過渡現象に触れる前に視聴することをお勧めします。

youtu.be

RLC回路の過渡現象について

それではRLC回路の過渡現象解析について説明していきたいと思います。

過現象について説明した後、過渡現象の解析方法その具体的な例を示していきたいと思います。過渡現象とは、スイッチのオンオフなど回路の状態の急な変化に対して電流や電圧などがそれまで定常状態であったものに変化が生じ、別の定常状態に移行するまでの振る舞いのことを指しています。

例えば、以下の図の回路ではスイッチが2つともオフの状態では電流は流れません。そして、S1をオンにした直後に電流が流れることになります。その一方、S1をオンにしてから十分な時間が経過するとまた電流が流れなくなります。この、スイッチをオンにした直後に電流が流れる状態を過渡状態と言っています。

解析手順

解析は次の手順で行います。手順は3ステップで下図に示しています。

まず、キルホッフの法則に基づいて微分方程式を立式します。その次に、その微分方程式から一般解を導出します。

最後に、初期条件に基づいて定係数を決定します。これらによって電流や電圧の時間的な振る舞いを表現することができます。

RLC直列回路の例

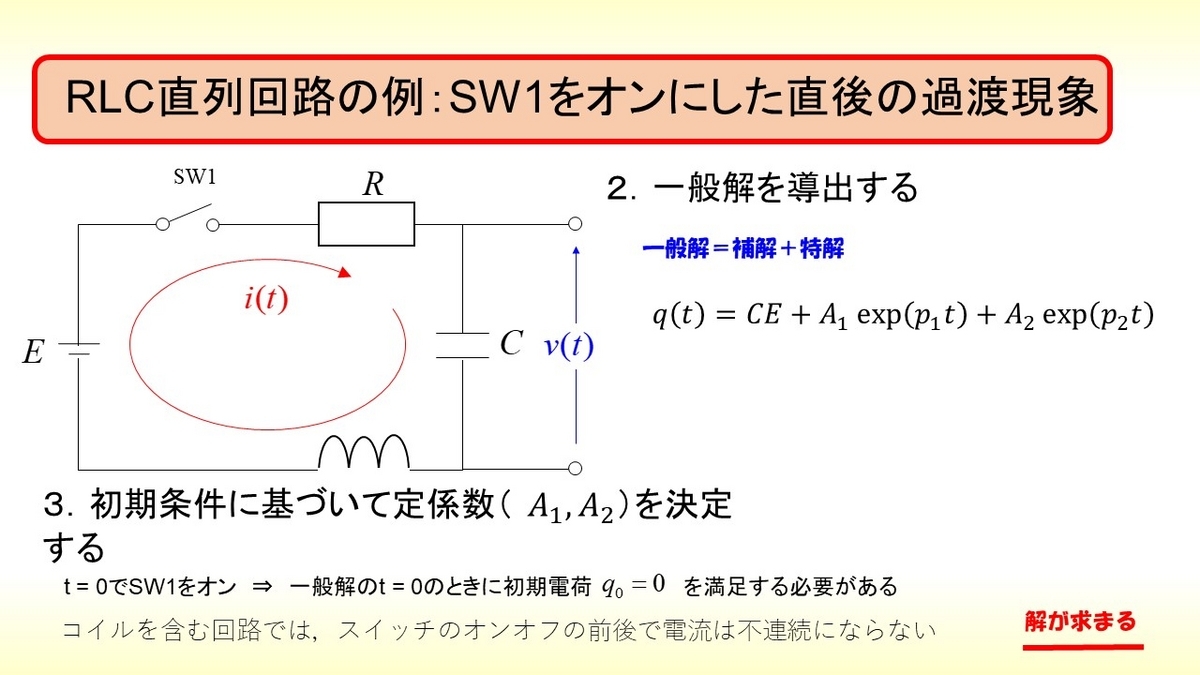
RLC直列回路の例を示したいと思いますSW1をオンにした直後の過渡現象を見ていきたいと思います。キルヒホッフの法則に基づいた微分方程式の立式を行いますが電圧則に基づくと次式が得られます。

$\displaystyle L \dfrac {di}{dt} + Ri+\dfrac {q}{C} = E$

ここで、電荷と電流の関係を用いることで次式を得ます。（2階の常微分方程式）

$\displaystyle L \dfrac {d^{2}q}{dt^{2}} + R \dfrac {dq}{dt} +\dfrac {q}{C} = E$

次に一般解を導出します。

まず、この微分方程式を満足する1つの解として特解を示します $q=CE$ で定常状態になっている状態を考えます。このとき、と $q$ の微分値並びに $q$ の2回微分値が0となります。よって、この微分方程式を満たすことになります。

次に他は特性方程式を解くことによって指数関数の係数が $p1,p2$ として求まります。また他には定数 $A_{1}, A_{2}$ が含まれます。

微分方程式の解について示した図（特解、補解、一般解） — 微分方程式の特解と補解

ここで得られた特解と補解とを足したものが一般解となります。ここで一般解には、まだ定まっていない係数 $A_{1}, A_{2}$ が含まれています。

最後に初期条件に基づいて低係数を決定します $T=0$ でスイッチをオンにしその際の初期電荷が0となります。

またコイルを含む回路においては、スイッチのオンオフ時に、その前後で電流は不連続になりません。この2つの条件によって定係数 $A_{1}, A_{2}$ を求めます。

以上の結果により電荷の過渡現象を解析的に求めることができます。

ここで得た結果を使いますと、電荷だけでなく電流電圧を求めることができます。具体的には電流は電荷の微分値でありますので、初期条件によって $A_{1}, A_{2}$ が定められた一般解について、その微分を求めることで電流 $i(t)$ を得ます。また、電圧は電荷をCで割ったものになりますので、 $v(t) = q(t)/C$ で求まります。