この記事ではモデル誤差抑制補償器（Model Error Compensator, MEC）についてまとめます。モデル誤差抑制補償器に関する動画・関連記事・関連論文・MATLABリンクは最下部に置いています。モデル誤差抑制補償器は，制御系のロバスト性を高める方法です。既存の制御系のロバスト性を高めたり，ノミナルの制御手法と併用してロバスト性を向上したりする目的で使用できます。本記事は以下の総合論文をベースにしてモデル誤差抑制補償器を紹介したものです。式展開や理論の詳細は原稿や最下部の関連論文をご覧ください。
執筆者：制御工学の研究を20年行っている国立大学教員
>>（総合論文，計測と制御PDF）モデル誤差抑制補償器を用いた既存制御系のロバスト化 (無料公開, J-Stage)
モデル誤差抑制補償器の概要
モデル誤差抑制補償器の制御目的は，入出力関係の意味でモデルの動特性に可能な限り近くなるよう制御システムの入出力特性を補償（ロバスト化）することであり，これによって，既存の制御系に外乱やモデル化誤差に対するロバスト性を付加することができます。補償器構造は単純なものであり，様々な制御システムと併用することができます。例えば，非線形系，非最小位相系，MIMO系などが対象例として挙げられます。また，PID制御やMPC（モデル予測制御）をはじめとする様々な制御方式と併用することも可能であり，良好なロバスト性能を実現することができます。制御工学分野で広く展開されている様々な理論と組み合わせるという視点に立つと、かなり多くの理論との相性が良いです。
モデル誤差抑制補償器は図に示すように，モデルPnと誤差補償器Dから成るシンプルな補償器構成です。最もシンプルなタイプのSISO，相対次数1かつ最小位相の制御対象を補償したい場合，誤差補償器Dは単なるハイゲインフィードバックで構成することができ，これにより見かけ上の入出力特性をモデルのものと（限りなく）近づけることが可能です。これにより，補償されたシステムを制御対象と見なして制御することで全体制御系が所望の制御を実現できます。より複雑なクラスの制御対象であっても，その設計の基本路線はハイゲインフィードバックであり，ノイズがある場合のトレードオフに基づいた設計論なども整備されています。
図はフィードフォワード補償器で制御する例であり，モデル誤差抑制補償器（MEC）で補償することにより制御対象のダイナミクスのバラツキの影響を抑制していることが見てとれます。
その他，ベンチマーク問題の適用や，電動車いす（搭乗者で動特性が大きく変わる）など様々な対象で有効性が示されています。
非線形システムのロバスト化
ここでは，非線形システム（非線形状態方程式）に対するモデル誤差抑制補償器の適用事例としてロバストなフィードバック線形化手法についての紹介を行います。非線形システムを制御する有力なアプローチの一つとして，線形化後に線形システムのための制御器を利用する方法が挙げられます。フィードバック線形化は非線形システムを線形化する手法であり，広く知られている手法です。一方，フィードバック線形化は非線形項を打ち消すことで線形化する方法であるためモデル誤差に弱く，モデル誤差がないことが利用の前提条件となっています。また，非線形システムの全ての状態量が必要になってきます。
これに対して，モデル誤差抑制補償器を用いればモデルに対するフィードバックを考えることで全体系をロバストに線形化することができます。また，出力フィードバック型のフィードバック線形化手法となっていることも本手法の特徴です。
非線形システムのロバスト化手法は例えば以下の論文をご覧ください。
モデル誤差抑制補償に基づく非線形システムのフィードバック線形化 (jst.go.jp)
モデル誤差抑制補償器に基づくロバスト経路追従制御 (jst.go.jp)
非最小位相系のロバスト化
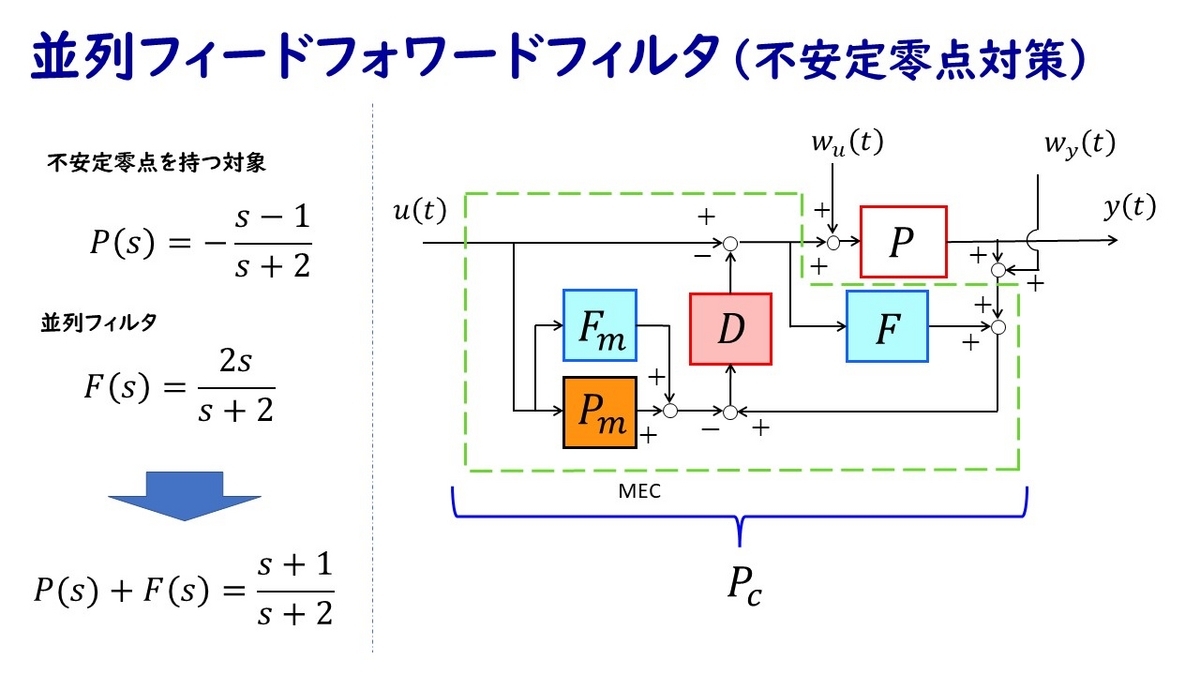
非最小位相系に対しては，モデル誤差抑制補償器を適用することはできますがハイゲインフィードバックは困難です。そのようなことから，誤差補償器Dの設計にも細かい知識なく設計法を提供すべく並列フィードフォワード補償器を併用した手法を提案しています。並列フィードフォワードフィルタの零点設定や誤差補償器を合わせた設計などの基本的な見通しはMEC単体に比べて良くなります。
非最小位相系のロバスト化は例えば以下の論文をご覧ください。
非最小位相系に対するモデル誤差抑制補償器の設計 (jst.go.jp)
既存制御システムとの併用例
既存制御システムとモデル誤差抑制補償器の併用は様々に挙げられます。PID制御やモデル予測制御，状態フィードバック制御などの既存手法と併用する併用例の図が以下になります。
外乱オブザーバとモデル誤差抑制補償器の比較
モデル誤差抑制補償器と外乱オブザーバとは，他手法との併用するスタンスやコンセプトが似ており，よく比較に挙げられます。外乱オブザーバ自体は，大石 潔先生，大西 公平先生により提案されており制御工学分野のみならず古くから汎用的に利用されている手法です。（例えば，外乱オブザーバの紹介）をご覧ください。）モデル誤差抑制補償器と外乱オブザーバの違いを以下にまとめます。
外乱オブザーバ
- 逆モデルが必要
- フィルタは（最小位相系の場合）ゲイン1，位相遅れ零に近いものを利用
モデル誤差抑制補償器
- 逆モデルが不要
- フィルタは（センサノイズが少なければ）ハイゲインのものを利用
同じ外乱抑制性能を満足させる上で，外乱オブザーバもモデル誤差抑制補償器もどちらでも設計でき，同等の性能を出せることが多いです。しかし，ノイズが多くなってくる場合や対象のモデル構造が複雑になる場合，フィルタのゲイン調整が双方で必要になります。場合によっては，ここの設計で性能が変わってきます。モデル誤差抑制補償器では，制御対象と誤差補償器の単純なループで設計を考えることになるため，既存のロバスト制御理論などの制御器設計理論の適用性は高いです。どちらを使用した方が良いかはケースバイケースになるかと思います。
モデル誤差抑制補償器では，逆モデルが不要な点で，非線形システムや非最小位相系・不安定な制御対象など適用クラスは広くとることができます。外乱オブザーバでも，非最小位相対応の研究などはされていますので，実装時にはどちらも試して良いものを選ぶというのが合理的です。
ロバスト制御とモデル誤差抑制補償器の関係
ロバスト制御は、制御工学分野で一時代を築いた重要な制御方策です。一般的なロバスト制御手法では，バラツキや外乱に特化して最悪性能の最適化という方向での展開を中心として研究が進められてます。問題設定としては，制御対象のバラツキの範囲で最悪性能を最適化するというのが設計方針になります。その結果，ノミナルだけでなく集合としての制御対象を取り扱う問題はかなり複雑になりロバスト性の向上は期待できるものの扱える評価関数の構造が限定的です。また，ロバスト指標以外の性能（例えばノミナル性能の向上）との両立は難しくなります。
その一方で，モデル誤差抑制補償器は，モデル誤差や外乱抑制性能のみに特化して設計でき，応答性能や追従制御性能などは既存の手法に任せる運用ができるため，汎用性が高くなります。もちろん，ロバスト制御かモデル誤差抑制補償器かという議論は正しくなく，モデル誤差抑制補償器に含まれる誤差補償器Dは，ロバスト制御の知見に基づいて設計することも可能です。
事例：PID制御システムのロバスト化
モデル予測制御との併用
モデル予測制御のようなモデルダイナミクスがベースとなって制御入力を設計するタイプの制御手法との親和性もある程度高いです。モデルの状態を使って制御入力の設計を行った上で，ロバスト性はモデル誤差抑制補償器によって担保することができます。
MATLAB
モデル誤差抑制補償器に関するMATLABコードはGithubに置いています。論文に対応したコードですので，論文と併せてご覧頂ければと思います。
基本制御系のMATLABコード
以下の２編の論文
"A design method of model error compensator for systems with polytopic-type uncertainty and disturbances(2021)"
"Model Error Compensator Design for Continuous- and Discrete-Time Non-minimum Phase Systems with Polytopic-Type Uncertainties(2022)"
に対応したMATLABコードはこちらです。
センサノイズとのトレードオフに基づく設計のMATLABコード
以下は，センサノイズ環境下でのモデル誤差抑制補償器の設計に対応したMATLABコードです。
GitHub - Hiroshi-Okajima/MATLAB_MEC02_sensor_noise: disturbance-rejection by MEC
並列フィードフォワード補償器との併用による非最小位相系・むだ時間系の補償のMATLABコード
並列フィードフォワード補償器を併用することで非最小位相系やむだ時間系のような誤差補償が難しい対象へのロバスト化が可能になります。
GitHub - Hiroshi-Okajima/MATLAB_MEC03_withPFC: control-systems
非線形システムに対するロバストフィードバッMATLABコードが以下になります。
信号制限フィルタのMATLABコード
MECの構造に基づいて提案した信号制限フィルタ（加速度制約や速度制約を満たすフィルタ）のMATLABコードが以下になります。
モデル誤差抑制補償器のビークル制御系への適用MATLABコード
以下は，モデル誤差抑制補償器に基づくロバスト経路追従制御に対応したMATLABコードです。
GitHub - Hiroshi-Okajima/Vehicle_control_MEC05
PID制御との併用に関するMATLABコード
以下は，モデル誤差抑制補償器とPID制御を併用したロバスト制御システムに関するMATLABコードです。
GitHub - Hiroshi-Okajima/MEC05-rengo2022
モデル誤差抑制補償器の動画・関連記事
以下はモデル誤差抑制補償器について説明している動画になります。30分で全体概要を説明している動画ですので是非視聴してください。
モデル誤差抑制補償器の関連記事はこちらです。
モデル誤差補償器 MATLABコード，動画まとめページ(google.com)
モデル誤差抑制補償器による既存システムのロバスト化（ロバスト性向上）｜岡島寛@熊大教員 制御note
川田先生のMECと外乱オブザーバの記事です。
研究業績
学術論文
これまでの研究業績はこちらです。
[18] 岡島寛，モデル誤差抑制補償器を用いた既存制御系のロバスト化，計測と制御，Vol. 62，No. 3，168-175 (2023)
[17] Ryuichiro Yoshida, Hiroshi Okajima and Takumi Sato, Model error compensator design for continuous- and discrete-time non-minimum phase systems with polytopic-type uncertainties, SICE Journal of Control, Measurement, and System Integration, Volume 15 Issue 2 pags 141-153 (T&F, Open Access)
[16] R. Yoshida, Y. Tanigawa, H. Okajima and N. Matsunaga, A design method of model error compensator for systems with polytopic-type uncertainty and disturbances，SICE Journal of Control, Measurement, and System Integration Volume 14, Issue 2 (2021) (Open access)
[15] Hiroshi Okajima,Yuta Nakabayashi and Nobutomo Matsunaga, Signal-Limitation Filters to Simultaneously Satisfy Constraints of Velocity and Acceleration Signals, SICE Journal of Control, Measurement, and System Integration，Vol.13, No.1, pp.1-8 (2020) (Open access)
[14] 岡島寛：ポリトープ型不確かさを有する連続時間線形時不変システムに対するモデル誤差抑制補償器のロバスト性能解析，計測自動制御学会論文集，Vol. 55, No. 12, (2019)
[13] 岡島寛，奥村洸祐，松永信智：モデル誤差抑制補償器を用いた車輪型倒立振子のロバスト速度補償，電気学会論文誌(C), Vol. 139, No. 3, (2019)
[12] 松永信智，坂本将一，田中友樹，岡島寛：モデル誤差抑制補償器を用いたSSV型パーソナルビークルの操縦支援制御系の設計と屋外走行評価，機械学会論文誌C編，Vol. 84，No. 858, 17-00349 (2018) j-stage
[11] 岡島寛，中林佑多，松永信智：任意信号に対して速度·加速度を制約する信号制限フィルタの設計，計測自動制御学会論文集，Vol.54, No.1，pp.146-152(2018) j-stage
[10] 奥村洸佑，岡島寛，松永信智：センサノイズ環境下でのモデル誤差抑制補償器の設計，システム制御情報学会論文誌，Vol.30，No.4，pp.153-155 (2017) j-stage
[9] G. Ichimasa, H. Okajima, K. Okumura and N. Matsunaga：Model Error Compensator with Parallel Feed-Forward Filter, SICE Journal of Control, Measurement, and System Integration，Vol.10, No.5, pp.468-475 (2017) (Open access)
[8] 岡島寛，松永信智：モデル誤差抑制補償器に基づくロバスト経路追従制御，システム制御情報学会論文誌，Vol.29，No.10，pp.466-468（2016） j-stage
[7] 菅野達也，壇裕介，岡島寛，松永信智：モデル誤差抑制補償器による福祉用パーソナルビークルのロバストな屋内隊列走行システムの走行評価，機械学会論文集(Ｃ),Vol.82, No.840, pp.15-00690 (2016) j-stage
[6] 岡島寛，一政豪，松永信智：非最小位相系に対するモデル誤差抑制補償器の設計，計測自動制御学会論文集，Vol.51, No.11, pp.794-801 (2015) j-stage
[5] 藤岡巧，岡島寛，松永信智：モデル誤差抑制補償器と周波数整形型終端状態制御の併用による3慣性ベンチマーク問題の一解法，計測自動制御学会論文集，Vol.50, No.12, pp.861-868 (2014) j-stage
[4] 岡島寛，西村悠樹，松永信智：モデル誤差抑制補償に基づく非線形システムのフィードバック線形化，計測自動制御学会論文集，Vol.50, No.12, pp.869-874 (2014) j-stage
[3] 梅井啓紀，岡島寛，松永信智，浅井徹：モデル誤差抑制補償器の多入出力システムに対する設計，システム制御情報学会論文誌，Vol.27, No.2, pp.67-72 (2014) j-stage
[2] 丸野裕太郎，A. T. Zengin，岡島寛，松永信智，中村憲仁：モデル誤差補償による福祉用前輪駆動型パーソナルビークルSTAVi の操縦特性の改善，JSME(C編), Vol.79, No.808, pp.4721-4733 (2013) j-stage
[1] H. Okajima, H. Umei, N. Matsunaga and T. Asai：A Design Method of Compensator to Minimize Model Error，SICE Journal of Control, Measurement, and System Integration, Vol.6, No.4, pp.267-275 (2013) (Open access)
解説記事(関連するもの）
[2] 岡島，松永：モデルと実対象の信号差を利用した制御，システム/制御/情報，Vol.60，No.2，pp.60-65 (2016)
[1] 岡島，松永：前輪駆動型電動車椅子に対する規範モデルに基づいた操縦性能改善，設計工学，Vol.50，No.4，pp.163-168 (2015)
国際会議
[14] H. Okajima, Model Error Compensator for adding Robustness toward Existing Control Systems, Preprints of the IFAC World Congress, pp. 3998 - 4005 (2023)
[13] R. Yoshida, Y. Tanigawa, H. Okajima and N. Matsunaga: A Design Method of Model Error Compensator using Meta-Heuristics and LMIs, Proceedings of the SICE Annual Conference 2020 pp. 1150-1155 (2020)
[12] Nobutomo Matsunaga, Naufal Bayu Fauzan, Hiroshi Okajima and Gou Koutaki, Archive Method of Stone Wall in Kumamoto Castle Lifted by Small CMG Crane using Model Error Compensator, 2019 12th Asian Control Conference , 18849231 (2019)
[11] Yuta Nakabayashi, Hiroshi Okajima, Nobutomo Matsunaga, Inter-Vehicle Distance Stabilization in Adaptive Cruise Control Using Signal Limitation Filter, Proceeding of 2018 IEEE International Conference on Systems, Man, and Cybernetics, pp.1985-1990 (2018)
[10] S. Sakamoto, T. Tanaka, H. Okajima and N. Matsunaga：Maneuverability evaluation of skid steer welfare vehicle for robust assistance control with model error compensator, Proceedings of ICCAS 2017 (2017)
[9] N. Matsunaga, H. Okajima and Y. Yamamoto：Robust variable stiffness control of McKibben type pneumatic artificial muscle arm by using multiple model error compensators, Proceedings of ICCAS 2017 (2017)
[8] Y. Nakabayashi, H. Okajima and N. Matsunaga：Signal limitation filter to satisfy velocity and acceleration constraints for arbitrary input signals, Proceedings of the SICE Annual Conference 2017
[7] T. Tanaka, H. Okajima and N. Matsunaga：Experiment of robust driving assistance control for skid steer welfare vehicle using model error compensator, Proceedings of ICCAS 2016 (2016) Outstanding Paper Award
[6] G. Ichimasa, K. Okumura, H. Okajima and N. Matsunaga：Extended structure of MEC for thermal process, Proceedings of the SICE Annual Conference 2016, pp.1593-1598 (2016)
[5] T.Sugano, H.Okajima and N.Matsunaga：Robust and precise platoon driving control of welfare vehicles along wheel track by using model error compensator, IECON2015, YF-001503
[4] T. Sugano, Y. Dan, H. Okajima, N. Matsunaga and Z. Hu：Indoor Platoon Driving of Electric Wheelchair with Model Error Compensator along Wheel Track of Preceding Vehicle, The 5th International Symposium on Advanced Control of Industrial Processes, 2014.5
[3] Y. Dan, H. Okajima, N. Matsunaga, Z. Hu and N. Nakamura：Experiment of Indoor Platoon Driving using Electric Wheelchair STAVi Controlled by Modeling Error Compensation System, ICT-PAMM Workshop on Mobility Assistance and Service Robotics, p26-31, 2013.11.
[2] Y. Maruno, Y. Dan, A. T. Zengin, H. Okajima and N. Matsunaga：Maneuverability Analysis of Front Drive Type Personal Vehicle STAVi using Modeling Error Compensation System, 7th IFAC Symposium on Advanced in Automative Control, 2013.9.
[1] H. Umei, H. Okajima, N. Matsunaga and T. Asai：A design method of compensator to minimize model error, SICE Annual Conference 2011, 2011.9.
他の研究グループにおけるモデル誤差抑制補償器の研究
他の研究グループにおけるモデル誤差抑制補償器の研究を特にタイトルにモデル誤差抑制補償器を含むものを中心として抜粋します。
T. Sano and S. Yamamoto, A Data-Driven Tuning Method for Model Error Compensator, Proc.of SICE 2018, 1199/2002 (2018)
H. Endo, R. Aramaki, K. Sekiguchi and K. Nonaka, Application of model error compensator based on FRIT to quadcopter, 2017 IEEE Conference on Control Technology and Applications (CCTA) (2017)
遠藤,関口,野中,モデル誤差補償器のオンライン調整法,計測自動制御学会論文集,55-3, 156/163(2019)
Y. Hatori, H. Nagakura, Y. Uchimura, Teleoperation with variable and large time delay based on MPC and model error compensator, IEEE International Symposium on Industrial Electronics(2021)
Y. Kawai, S. Nagao, Y. Yokokura, K. Ohishi,T. Miyazaki, Quick Torsion Torque ControlBased on Model Error Compensator and Disturbance Observer with Torsion Torque Sensor,IEEE/SICE International Symposium on SystemIntegration 2021 (2021)
S. Wakitani and T. Yamamoto, Design of a Database-Driven Model Error Compensator inSmart Model-Based Development, InternationalConference on Advanced Mechatronic Systems(2021)
鈴木元哉,制御入力速度飽和した初期実験データによるビークルのデータ駆動予測型制御器調整,電気学会論文誌C編,142-8, 959/970 (2022)
M. Suzuki and S Yahagi, Data-driven Design of Model Error Compensator and Fictitious Reference Signals for Vehicle Velocity Control of Autonomous Driving, 2022 22nd International Conference on Control, Automation and Systems (ICCAS) (2022)
川田昌克,モデル誤差抑制されたPID制御系のFRITを利用したパラメータ調整とLEGO教材による実験的検証,システム制御情報学会論文誌,Vol.37,No.1,31/33(2024)
零点と不安定極をもたない2次系に対する外乱オブザーバとモデル誤差抑制補償器の関係について, 計測自動制御学会論文集, Vol. 60, No. 2, 101/103 (2024)
K. Shikada and N. Sebe, Relation between disturbance observer and model error compensator, 2023 SICE ISCS (2023)
脇谷伸, スマートMBDアプローチに基づく制御システム設計—モデルとデータを融合した新しいデジタルものづくりを目指して, システム/制御/情報, Vol. 67, No 8 pp. 343-348 (2023)
吉田, 石川, 南, データ駆動型フィードバック変調器による非線形補償器の設計, 計測自動制御学会論文集, Vol. 59, No. 5, pp. 252-258 (2023)
国内会議
（2024以降）
板宮敬悦，モデル誤差抑制補償要素を併用した適応制御系に関する研究，MSCS2024
板宮 敬悦，ロバストモデル規範形適応制御系における固定補償要素のモデル誤差抑制制御器としての役割，SCI 2024
菅原貴弘，脇谷伸，山本透，落岩崇，富山秀樹，機械システムに対するGMV-MECの適用検討，MSCS2024
以上がモデル誤差抑制補償器に関する関連記事になります。本記事は以上です。これらの内容に基づいて更なる研究の進展や，実応用がされれば幸いです。モデル誤差抑制補償器の汎用性（様々なタイプのシステムへの適用可能性）は高いので更なる研究への展開への可能性は大きいと考えています。
自己紹介
岡島 寛 （熊本大学工学部情報電気工学科准教授）
制御工学の研究をしています。モデル誤差抑制補償器，状態推定，量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル（伝達関数・状態方程式・MATLABなど）
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。
