この記事では制御のむだ時間についてまとめます。むだ時間は、プロセス系を中心として様々な対象で現れるものであり、その制御は難解です。本記事では、むだ時間の特徴や近似表現、むだ時間を含むシステムの制御手法について触れたいと思います。
本記事の関連記事としては、不安定零点と制御に関する以下のものが挙げられます。
むだ時間系の表現
むだ時間は、入力信号がシステムに印加された後、印加した入力の影響が一定時間経過してから出力信号に反映されるような場合の応答開始までの時間差のことを表します。プロセス系や信号の伝送過程における遅延など様々な要因で生じます。制御入力をとし、むだ時間長さを
とすると、入力むだ時間を含むシステムの伝達関数表現は有理関数
を使って次のように表すことができます。
\begin{equation}y(s) = P(s)e^{-Ls} u(s)\end{equation}
と表現され、制御システムと表記される無限次元系として表されます。
むだ時間系の応答波形
まず、応答波形を確認してみます。むだ時間がないシステムとむだ時間を含むシステム
との比較図が以下の通りです。ただし、
とし、
としていますので、有理関数部分は全く同じです。ここでは
となっています。
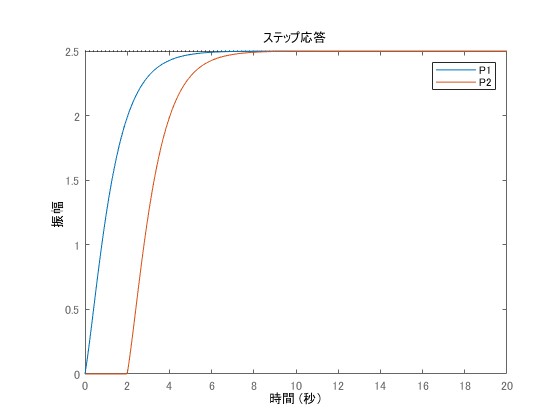

むだ時間系の応答波形を確認すると、各時刻の値が2秒づつ右にシフトしていることがそれぞれ確認できます。
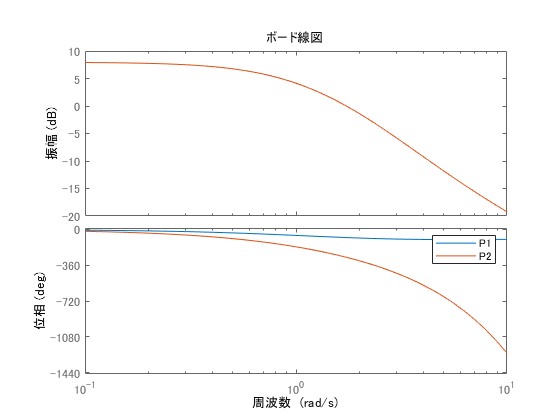
むだ時間系のボード線図
次にと
のボード線図を示します。
に比べてむだ時間を含む
では位相が遅れていることがわかります。特に、この遅れは周波数が高いほど大きくなっています。他方、ゲイン線図は
と
で重なっており、ゲインの周波数特性が同じであることがわかります。
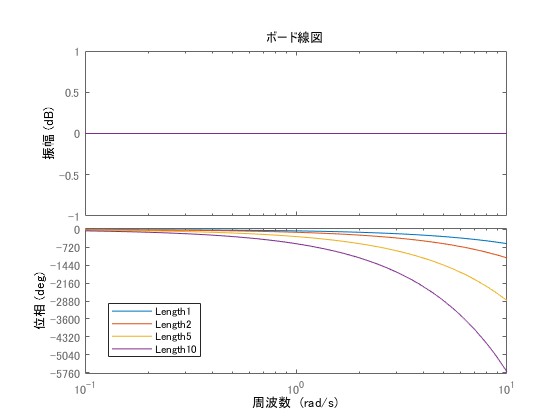
むだ時間項について
でボード線図を描くと次のように与えられます。
むだ時間系の状態方程式表現
印加された制御入力が一定時間経過後に対象に影響を与える場合を入力むだ時間、出力が観測されるまでにタイムラグがある場合を出力むだ時間といいます。両者ともに上記の伝達関数表現がなされますが、状態空間表現においては入力むだ時間を含むシステムは
\begin{eqnarray}
\dot x (t) &=& Ax(t) + Bu(t-L)\\
y(t) &=& Cx(t)+Du(t-L)
\end{eqnarray}
と表記され、出力むだ時間を含むシステムは
\begin{eqnarray}
\dot x (t) &=& Ax(t) + Bu(t)\\
y(t) &=& Cx(t-L)+Du(t-L)
\end{eqnarray}
と表記されます。
フィードバック制御
むだ時間長さが長いほど制御が難しくなることが知られています。まず、単純に
にフィードバック制御を施す場合を考えます。このとき、単位フィードバックを施すと次のシステムが得られます。
\begin{eqnarray}
G(s) = \frac{P(s)C(s)e^{-Ls}}{1+P(s)C(s)e^{-Ls}}
\end{eqnarray}
このシステムにおける極は無限個現れることになります。これがむだ時間系の特徴です。
むだ時間の近似と不安定零点
無限次元系が都合が悪くむだ時間を有理伝達関数で表現する場合にはパデ近似がよく用いられます。例えば、1次のパデ近似でむだ時間長さ秒のむだ時間要素
を表すとき次のように近似されます。
\begin{equation}
e^{-Ls} \simeq \left(\frac{1-Ls/2}{1+Ls/2}\right)
\end{equation}
このとき、近似されたむだ時間要素には不安定零点が現れていることが確認できます。パデ近似は
の
近傍での有理関数近似であり、低周波数から合わせる形の近似となっています。1次のパデ近似が用いられることが多いですが2次のパデ近似も次のように与えられます。
\begin{equation}
e^{-Ls} \simeq \left(\frac{1-Ls/2+L^2s^2/12}{1+Ls/2+L^2s^2/12}\right)
\end{equation}
また、むだ時間を含むシステムをフィードバックすると無限個の極が表れて設計の見通しが悪いことからスミス法や内部モデル制御などでむだ時間項の影響が出力に現れないような設計がなされます。
むだ時間系の制御手法
状態予測制御
入力むだ時間系では、印加された入力信号が状態に影響を与えるまでに秒を要します。このとき、
秒先の状態がわかれば状態フィードバックによって入力むだ時間系の制御ができます。状態予測制御では、状態の
秒先の予測値を求め、それを利用して状態フィードバック制御を施します。具体的には、現時点での状態
がわかっているものとし、現在から過去
秒前までの間で印加した入力を利用することで、状態
の時間発展を計算することが可能となります。具体的には、状態
の
秒での推定値
を状態方程式の解の公式を利用して次のように求めます。
これにフィードバックゲインを掛けた入力
\begin{equation}
u(t) = K\tilde x(t+L)
\end{equation}
を印加することを想定すれば、(むだ時間分の遅れはあるものの)通常の線形時不変系の安定化と同じ枠組みでフィードバックゲインを設計した場合と同等の応答が得られます。
スミス補償器
むだ時間系に対する有力な制御アプローチとしてスミス補償器が知られています。ここではその紹介を行います。スミス補償器は、制御対象の伝達関数のモデルを制御器内部に用います。記号として区別するためにモデルを
と表記します。
以下にスミス補償器の構造を示します。
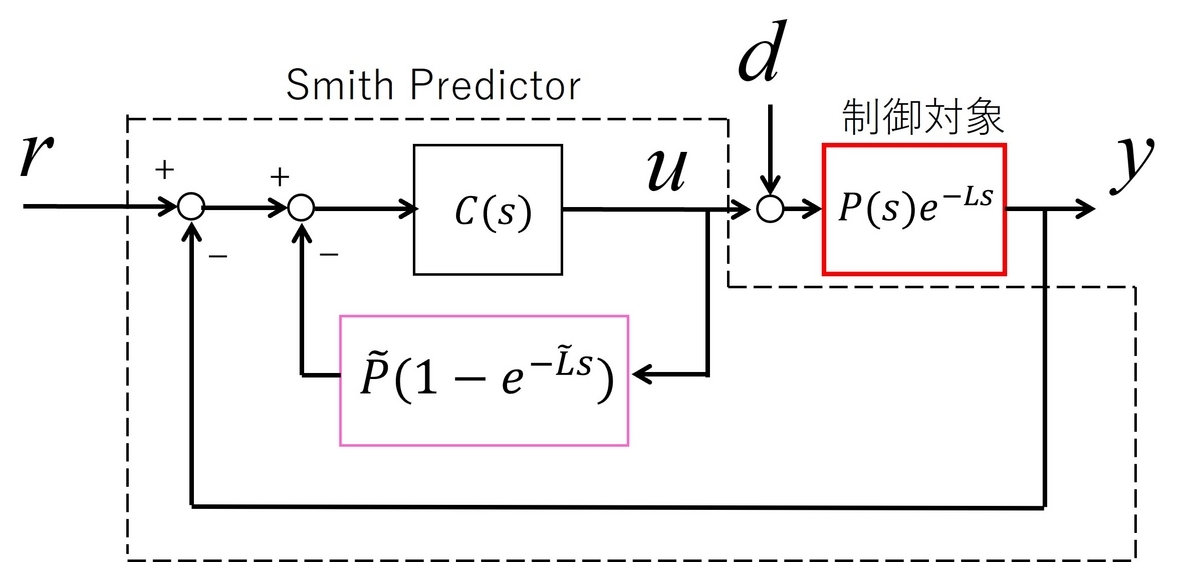
ここで、モデルの各パラメータ値が正しく求まっているものとし、、
とするとスミス補償器を適用した制御系の応答は次のように与えられます。
\begin{eqnarray}
y(s) = \frac{P(s)C(s)e^{-Ls}}{1+P(s)C(s)}r(s)+\frac{Pe^{-Ls}+P(s)C(s)(1-e^{-Ls})P(s)e^{-Ls}}{1+P(s)C(s)}d(s)
\end{eqnarray}
ここで、閉ループ極は有限個となりむだ時間がない場合の設計ができるため設計見通しが良いです。他方、モデルの精度やむだ時間長さの精度が悪い場合には、想定と異なった振る舞いになることから注意が必要です。
また、スミス補償器では制御対象のむだ時間がフィードバックループに与える影響を除去することができるものの、制御対象のむだ時間そのものを打ち消すわけではないことに注意が必要です。を見てもわかるようにむだ時間
の項が残っており、これは制御器
によって消せるものではありません。
むだ時間の関連動画・関連記事
以下はむだ時間について説明している動画になります。
むだ時間系の関連書籍
むだ時間系の書籍はこちらになります。明治大の阿部先生、東京都立大の児島先生の共著です。
また、むだ時間を含むシステムについて、例えば以下の書籍でも説明されています。
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島寛 (システム制御 control-theory.com)
English Web Page
Hiroshi Okajima (Control Engineering control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。
以上が**に関する関連記事になります。本記事は以上です。

