この記事では状態方程式表現されたシステムの同値変換(等価変換,座標変換)についてまとめます。状態方程式の同値変換について説明した動画は最下部に置いています。
なお、状態フィードバック制御の全体像は次の記事でまとめています。
状態方程式の表現
まず制御対象のダイナミクスが、次図の状態方程式表現として与えられている場合を考えます。状態方程式に基づく制御は、制御工学分野の基礎的な内容の一つです。

制御入力はu、制御出力はyであり、状態を x とします。そして n が制御対象の次数であり、状態ベクトルの要素数は n となります。
また A, B, Cはそれぞれ n次 の正方行列、1 入力の場合には、Bがn次の縦ベクトル。もし、多入力の場合には Bは行列の形になります。Cは 1 出力の場合は n次の横ベクトルとなります。
同値変換(座標変換)の概要
同値変換においては、状態 x に関する状態方程式を変換して \tilde x に関する状態方程式への変換を考えます。同値変換は、座標変換とも等価変換とも言えます。ここでは同値変換として説明を進めます。

ここで、図において、行列Tは正則な行列であり、逆行列を持つものを与えます。このとき、行列 T を用いることで、状態の座標の取り方を変えるということになります。これによって同じ入出力特性を満足するような、別の状態 \tilde x に関する状態方程式を、同値変換で得ることができます。
同値変換の前後で保存される性質
この同値変換の前後で、以下の性質が保存されます。
まず、一つ目ですが、入出力特性が保存される変換であるため、両者を伝達関数に変換したものがそれぞれで一致します。
2番目の極については、伝達関数が一致することからも明らかですが、両者の極が一致しており、行列Aと行列 \tilde Aの固有値が完全に一致します。
3番目は、同値変換前のシステムが可制御なら同値変換後も可制御、同値変換前が不可制御なら同値変換後も不可制御と性質が保存されます。

状態方程式の同値変換手順
そして同値変換の方法を説明します。下図で、同値変換の流れを示しています。

まず最初に状態方程式が与えられた時、状態変換
![]()
と与えます。このとき、Tの逆行列を使って以下も成り立ちます。
![]()
ここで、式を両辺を時間で微分すると
![]()
が得られます。
これを踏まえてステップに移ります。
元の状態方程式に、上述の2式を代入すると、ステップ1に記載した式が得られます。そして、ステップ1で得られた式に、両辺の左側からTの逆行列をかけることによってステップ2を得ます。そして
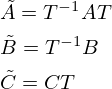
とすることで同値変換が完了します。なお、直流成分(直達項)がある場合は変換の前後でDは変わりません。
同値変換のメリット
可制御正準形
最後に、同値変換のメリットを説明して終わりたいと思います。同値変換をすることによって、設計や解析の見通しが良い枠組みで考えることができる、というメリットがあります。例えば、もともとのシステムが可制御な場合には、同値変換によって可制御正準系の変換をすることができます。これにより、極配置等を簡単に実現することができます。
対角正準形
また対角正準系の変換をすることでシステムのモードの
関係をしっかり調べることができます。

以上で同値変換に関する説明を終わります。
状態方程式の同値変換に関する動画
関連ページ(同値変換)
>>制御工学チャンネル:500本以上の制御動画ポータルサイト Control Engineering Channel - 01-Prof.Okajima (control-theory.com)
自己紹介
岡島 寛 (熊本大学工学部情報電気工学科准教授)
制御工学の研究をしています。モデル誤差抑制補償器,状態推定,量子化制御など
研究室HP
岡島研究室(システム制御 control-theory.com)
制御動画ポータルサイト
制御工学チャンネル(伝達関数・状態方程式・MATLABなど)
電気動画ポータルサイト
本記事をお読みいただきありがとうございます。役に立った、と思われましたら、ブックマーク・シェア等のアクションをしていただければ嬉しいです。