部分分数分解：逆ラプラス変換や対角正準形の導出に利用

本記事では部分分数分解についてまとめます。部分分数分解により有理関数を分解する方法とその制御工学分野での利用についての説明を行います。部分分数分解について説明した動画や関連記事リンクは最下部に置いています。

部分分数分解の概要
簡単な部分分数分解と信号波形の例
部分分数分解の方法
- 部分分数分解による応答計算
- 部分分数分解を利用した対角正準形の導出
部分分数分解の動画・関連記事
- 関連記事
- 自己紹介

部分分数分解の概要

制御工学において、ラプラス変換表により逆ラプラス変換を行うことで信号波形を得ます。信号のラプラス変換は $s$ の有理関数として与えられ、その信号が一次式や二次式の場合にはラプラス変換表により逆ラプラス変換で波形が求まります。他方、より高次の場合には、まず、有理関数として与えられた信号のラプラス変換に対して部分分数分解を施し、一次式もしくは二次式まで分解することにより、それぞれの項に対して逆ラプラス変換を施すことができ、信号波形が（時間の関数として）得られます。

簡単な部分分数分解と信号波形の例

ここでは、簡単な例を一つ示します。制御対象（伝達関数表現） $P(s) = 1/(s+2)$ に対して、単位ステップ入力（のラプラス変換） $r(s) = 1/s$ を印加したとき、制御出力は次式で与えられます。

\begin{equation} y(s) = P(s) r(s) = \frac{1}{(s+2)s} \end{equation}

このとき、 $1/(s+2)s$ は次の形式に分解できます。

\begin{equation} \frac{A}{s+2}+\frac{B}{s}\end{equation}

ここで、 $A = -1/2$ 、 $B = 1/2$ とすると以下の等号が成り立ちます。

\begin{equation} \frac{1}{(s+2)s}=-\frac{1}{2}\frac{1}{s+2}+\frac{1}{2}\frac{1}{s}\end{equation}

ここで、 $y(t)$ を求めたいとき、上の式に基づいて、それぞれの項を逆ラプラス変換することで導出できます。

\begin{equation} y(t) = -\frac{1}{2} e^{-2t} + \frac{1}{2}\end{equation}

ここでは、分母多項式の次数が2のケースを扱っていますが、より高次の場合についても低次の項へと分解することで結果への見通しを良くすることができます。

部分分数分解の方法

有理関数 $Q(s)$ は次の形で与えられます。

\begin{equation} Q(s) = \frac{N(s)}{D(s)}\end{equation}

ここで、 $N(s), D(s)$ はそれぞれ $s$ の多項式です。部分分数分解では $Q(s)$ を簡単な部分分数の和に分解します手順は以下の通りです。

分母の因数分解

最初に、 $D(s)$ の因数分解を行います。例えば次のような形で分解されます。

\begin{equation} D(s) = (s+a_1) (s+a_2) (s^2 + a_3 s+ b_3) (s+a_4)^2\end{equation}

部分分数分解後の形式

分母の因数分解を行った結果として次の形式で分解されます。

\begin{equation} Q(s) = \frac{A}{s+a_1} + \frac{B}{s+a_2} + \frac{Cs+D}{s^2+a_3s+b_3}\\ + \frac{E}{s+a_4}+\frac{F}{(s+a_4)^2}\end{equation}

このとき、正しく $A, B, C, D, E, F$ を求めれば等号が成り立ちます。

係数の求め方

基本的に、両辺を同じ分母で通分して分子の係数同士を比較して方程式を立て、その連立方程式を解くことで $A, B, C, D, E, F$ を求めることができます。

また、1次因子については、次の方法で係数を求めることができます。ここでは係数 $A$ を求めてみます。

$Q(s)$ に $(s+a_1)$ を掛ける。
1.で得た $(s+a_1)Q(s)$ において $s \rightarrow -a_1$ を取ったものが $A$ となる。

実際、 $Q(s)$ に $(s+a_1)$ を掛けたとき、分解した式において右辺は $A + \cdots$ となり、 $A$ 以外は $(s+a_1)$ の一次式になります。そのため、 $s=-a_1$ を代入すると右辺では $A$ 以外の項はゼロとなります。

部分分数分解による応答計算

制御対象 $P(s)$ のステップ応答を部分分数分解を利用して導出します。制御対象は

\begin{equation} P(s) = \frac{s+3}{s^2+3s+2}\end{equation}

と与えられ、 $r(s) = 1/s$ を印加します。

このとき、 $y(s) = P(s)r(s)$ は次のように記述できます。

\begin{equation}y(s)=\frac{s+3}{s^3+3s^2+2s}\end{equation}

ここで、因数分解を行い次の形式を得ます。

\begin{equation} y(s) = \frac{A}{s+1}+\frac{B}{s+2} + \frac{C}{s}\end{equation}

このとき、 $A, B, C$ はそれぞれ次のように得られます。

\begin{equation} A = \lim_{s\rightarrow -1}(s+1)\frac{s+3}{s^3+3s^2+2s}\\=\lim_{s\rightarrow -1}\frac{s+3}{s^2+2s}=-2\end{equation}

\begin{equation} B = \lim_{s\rightarrow -2}(s+2)\frac{s+3}{s^3+3s^2+2s}\\=\lim_{s\rightarrow -2}\frac{s+3}{s^2+s}=\frac{1}{2}\end{equation}

\begin{equation} C = \lim_{s\rightarrow 0}s\frac{s+3}{s^3+3s^2+2s}\\=\lim_{s\rightarrow 0}\frac{s+3}{s^2+3s+2}=\frac{3}{2}\end{equation}

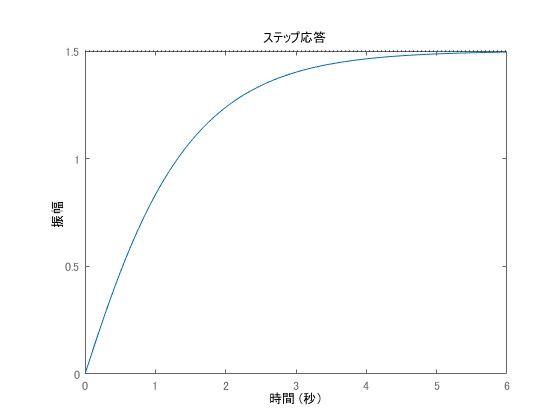
結果として、出力 $y(t)$ は次のように求められます。

\begin{equation}y(t) = 2e^{-t}-\frac{1}{2}e^{-2t}+\frac{3}{2}\end{equation}

実際に以下の出力波形と一致します。

部分分数分解を利用した対角正準形の導出

次に、部分分数分解を用いたシステム $P(s)$ の状態空間表現への変換を行います。対象は以下で与えられるものとします。

\begin{equation} P(s) = \frac{s+3}{s^2+3s+2}\end{equation}

このとき、 $P(s)$ を部分分数分解すると

\begin{equation} P(s) = \frac{A}{s+1}+\frac{B}{s+2}\end{equation}

とすることができ、 $A, B$ は次のように求まります。

\begin{equation} A = \lim_{s\rightarrow -1}(s+1)\frac{s+3}{s^2+3s+2}\\=\lim_{s\rightarrow -1}\frac{s+3}{s+2}=2\end{equation}

\begin{equation} B = \lim_{s\rightarrow -2}(s+2)\frac{s+3}{s^2+3s+2}\\=\lim_{s\rightarrow -2}\frac{s+3}{s+1}=-1\end{equation}

結果 $P(s)$ は次のように記述できます。

\begin{equation} P(s) = \frac{2}{s+1}-\frac{1}{s+2}\end{equation}

それぞれ独立した状態を使って対角正準形として記述すると制御対象 $P$ の状態方程式は次のように記述できます。

\begin{equation} \dot x (t) = A x(t) + B u(t) \\ y(t) = Cx(t)\end{equation}

ただし、 $A, B, C$ はそれぞれ

\begin{equation}A = \begin{bmatrix} -1 & 0\\0 &-2\end{bmatrix}, B = \begin{bmatrix} 1 \\1\end{bmatrix}, C = \begin{bmatrix} 2 & -1\end{bmatrix}\end{equation}

で与えられます。