制御システムにおける極零相殺について

この記事では極零相殺についてまとめます。伝達関数、極、零、および極零相殺は、制御システムの解析と設計において基本的かつ重要な概念です。これらを正確に理解し、適切に扱うことで、システムの安定性や応答特性を効果的に管理することが可能になります。ここでは、極零相殺によるシステム簡略化と極零相殺において注意すべき点について触れます。

伝達関数に基づく制御の全体像はこちら

blog.control-theory.com

伝達関数
関連記事
線形システムに関する書籍

伝達関数

伝達関数は、線形時不変システム（LTIシステム）における入力と出力の関係を周波数領域で表す数学的なツールです。具体的には、システムへの入力とその出力との間の関係を、複素変数 $s$ の関数として表現します。システムの微分方程式をラプラス変換することで導かれ、次のように定義されます。

\begin{equation} G(s) = \frac{Y(s)}{U(s)}\end{equation}

ここで、 $G(s)$ は伝達関数、 $Y(s)$ は出力のラプラス変換、 $U(s)$ は入力のラプラス変換です。伝達関数は、システムがどのように振る舞うか、特に入力に対する出力の応答を解析するために非常に有用です。

極と零点について

極（Poles）: 伝達関数の分母多項式をゼロにする $s$ の値を「極」と呼びます。極はシステムの動的特性、特に自然振動数や減衰特性に関係します。極の位置は、システムの応答が安定しているかどうかを判断するために重要です。極が右半平面に一つでも存在する場合、そのシステムは不安定となります。
零点（Zeros）: 伝達関数の分子多項式をゼロにする $s$ の値を「零点」と呼びます。零点は特定の周波数におけるシステムの応答を抑制または強調する役割を果たします。零点の位置は、入力信号のどの成分がどのように出力に影響するかを決定します。

極零相殺（Pole-Zero Cancellation）とは

極零相殺とは、伝達関数の極と零点が全く同じ位置に存在し、それらが互いに打ち消し合う現象を指します。具体的には、伝達関数 $G(s)$ が以下のような形を持つとします。

\begin{equation} G(s) = \frac{(s - z_1)(s - z_2)}{(s - p_1)(s - p_2)} \end{equation}

ここで、もし $z_1 = p_1$ であれば、極 $p_1$ と零 $z_1$ はキャンセルされ、伝達関数は次のように簡略化されます。

\begin{equation} G(s) = \frac{(s - z_2)}{(s - p_2)}\end{equation}

このような極零相殺により、システムの伝達関数が単純化される場合があります。しかし、実際の物理システムにおいて完全な極零相殺が起こることは稀で、微小なズレがシステムの応答に影響を及ぼす可能性があります。また、極零相殺が起きると、システムの内部の動作が観測されない「不安定な挙動」を引き起こす

場合があります。これは、システムの内部挙動が完全には反映されないため、システムの制御が難しくなる可能性があります。

極零相殺が制御システムに与える影響は深刻な場合があり、特に制御系設計において意図的に極零相殺を行う際は、その結果として生じる可能性のある制御性能の低下や不安定性を慎重に評価する必要があります。

安定な極零相殺

ここで、状態空間表現を考えます。

\begin{equation} A = \begin{bmatrix} -1 &0\\0&-2\end{bmatrix}, B = \begin{bmatrix} 1\\1\end{bmatrix}, C = \begin{bmatrix} 1-\epsilon & \epsilon \end{bmatrix}\end{equation}

ここで与えられた係数を持つシステムは2次であり、その伝達関数は次式で与えられます。

\begin{equation} G(s) = \frac{1-\epsilon}{s+1}+\frac{\epsilon}{s+2} = \frac{s+(2-\epsilon)}{(s+1)(s+2)}\end{equation}

このとき、 $\epsilon = 0$ において安定極と零点が相殺し、極零相殺が生じます。ここで、 $\epsilon$ を様々に変えたステップ応答を見てみます。 $\epsilon$ を0.1刻みで-0.4から+0.4まで動かした応答波形がこちらです。

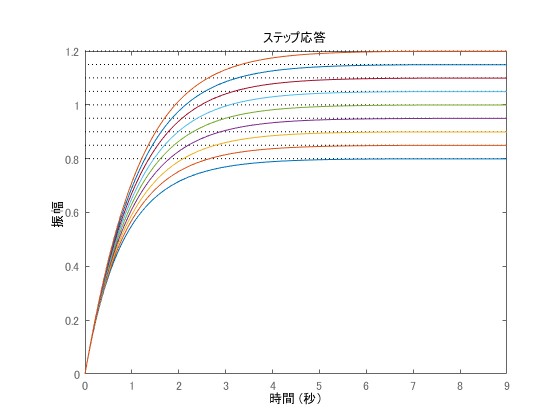
真ん中の緑色が極零相殺の応答波形になりますが、他の応答波形から劇的に変動があったわけでないことがわかります。仮に、 $\epsilon = 0$ の場合、このシステムは不可観測となります。つまり、システムの観測できないモードが存在するといえます。

不安定な極零相殺

特に、 $z_1$ および $p_1$ の実部が正である場合、不安定な極零相殺と呼びます。先ほどの例から少し変更して、 $A$ 行列の極を不安定にしました。

\begin{equation} A = \begin{bmatrix} -1 &0\\0&2\end{bmatrix}, B = \begin{bmatrix} 1\\1\end{bmatrix}, C = \begin{bmatrix} 1-\epsilon & \epsilon \end{bmatrix}\end{equation}

このとき、 $\epsilon = 0$ とすると、入出力システムは安定ですが、観測できないモードが不安定となります。 $\epsilon \neq 0$ では、どれだけゼロに近い値でも入出力システムは不安定となります。

非線形システム

非線形システムを入出力線形化した場合、システムの次数 $n$ とシステムの相対次数 $m$ に次数差が存在していると、入出力には表れないダイナミクスが内部に存在することになります。一見して、入出力関係が安定化されていても、その内部ダイナミクスが不安定となる場合があります。（出力）零ダイナミクスが不安定なことは、線形系の不安定な極零相殺に関連してきます。