This article discusses control methods for systems with unstable zeros. Characteristics and limits of the system with unstable zeros are introduced.
- Unstable Zeros
- Representation of Systems with Unstable Zeros
- Inverse Response and Zeros
- Performance Limits of Non-Minimum Phase Systems
- Characteristics in Frequency Response of Non-Minimum Phase Systems
- Related Videos and blogs on Unstable Zeros
Unstable Zeros
Below is an example of a transfer function of a control object with unstable zeros.
![]()
In a transfer function, a zero is an solution that satisfies [Numerator Polynomial] = 0. The zero of the first object is
, and the zero of the second object is
. Both solutions have positive real parts. If there is even one unstable zero among the zeros, control becomes extremely difficult.
Examples of Systems with Unstable Zeros
In control system design, attention is often focused on the poles of the control system. However, even if the poles of the control system are placed to achieve an appropriate damping ratio, the time response may not match the expected waveform. This is related to the zeros of the control object, and it can be said that the zeros of the control object represent the potential capabilities and limitations that can be realized by feedback control. Particularly, when a control object has unstable zeros, it is often challenging to achieve good responses in the design of control systems.
Unstable zeros frequently occur in rockets, airplanes, and process control systems where sensors and actuators tend to be non-collocated. Additionally, due to the difficulty of control, the inverted pendulum, which possesses unstable poles and zeros, has long been used as a control object.
Representation of Systems with Unstable Zeros
When a control object has N unstable zeros, the following representation provides a good overview.
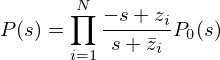
are the unstable zeros, and
is a stable and minimum-phase transfer function.
About the Inverse System
For objects with unstable zeros, the inverse system becomes unstable. Specifically, for the above , the inverse of the unstable zeros becomes unstable poles, making it impossible to construct an inverse system for objects with unstable zeros, so approximate handling is done. Specifically, if we consider the system where the inverse system of
is multiplied by the above
, it will function as an inverse system at low frequencies.
Inverse Response and Zeros
One phenomenon that occurs in systems with unstable zeros is the inverse response. Below is an example of a response waveform.

This is a result of applying a step signal, where the output signal eventually converges to 1. However, around time 0 seconds, it initially moves in the opposite direction (downward) from the convergence value before moving towards a positive value. This type of response is called an inverse response (or undershoot).
In systems with unstable zeros, an inverse response occurs. Particularly, when there is one unstable zero, it is known to initially move in the opposite direction from the convergence value at time 0. The initial oscillation changes depending on the number of unstable zeros. Detailed explanations on this can be found in the following literature.
>>Zeros in Control Systems (jst.go.jp)
Performance Limits of Non-Minimum Phase Systems
For control objects with unstable zeros, there are limits to control performance. Specifically, in target tracking control, the tracking error ideally should be zero. Control that always results in a tracking error of 0 is called perfect tracking. Such control is achievable in minimum-phase systems but is impossible with unstable zeros. The achievable control performance depends on the values of the zeros. For example, in the following literature, the lower bound of the 2-norm of the tracking error is estimated.
>>Analysis of Tracking Performance Limits for a Class of Reference Signals (jst.go.jp)
In the case of step targets, it is characterized as follows:
For the control object , when designing a controller for tracking a step target
, the lower bound of the tracking error is given by:
\begin{equation}J = \inf \|e\|_2^2 = \sum_{i=1}^k \frac{2Re(z_i)}{|z_i|^2} \end{equation}
The closer the unstable zeros are to the origin and the more there are, the harder it is to track (the larger the tracking error).
In addition, the following literature explains parallel feedforward compensators and the relationship with zero dynamics in nonlinear systems.
>>Unstable Zeros and Control (jst.go.jp)
Characteristics in Frequency Response of Non-Minimum Phase Systems
When there are unstable zeros, there is a characteristic of a sudden phase change at certain frequencies. Especially in the inner-outer decomposition, the inner part exhibits a sudden phase change without a change in gain.
Related Videos and blogs on Unstable Zeros
Blogs
Videos (in Japanese)