This article summarizes the controllability and observability of systems. First, I would like to discuss controllability. Links to videos explaining controllability and observability are provided at the bottom.
The overall picture of state feedback control is summarized in the following article.
Summary of State Feedback Control and Control Based on State Equations
- State Equation Representation
- Controllability of the System
- Observability of the State Equation
- Videos Related to Controllability and Observability
- Related Pages (Controllability and Observability)
State Equation Representation

The state equation representation of the control object is as shown in the above figure. In the state equation, the control input is u, and the control output is y. The state vector is expressed as x, with n elements.
The system's order is expressed using the symbol n, and for an n-order system, the matrix A is an n-order square matrix. B is an n-order column vector for single-input systems, and it takes the form of a matrix if there are multiple inputs.
C is an n-order row vector, and it takes the form of a matrix if there are multiple outputs.
Controllability of the System
First, I will explain controllability. Controllability is an index that expresses whether the state can be freely moved by input, and it is one of the important matters in the field of control engineering. If a system is controllable or stabilizable, it can be stabilized by state feedback. For example, if state feedback control u = -Kx is applied to the control object, then
\begin{equation} \dot x (t) = (A-BK)x(t) \end{equation}
The autonomous system is obtained. If the real parts of the eigenvalues of A-BK are negative, the autonomous system is stable. If the system is controllable or stabilizable, then such a K can be found.
Here, it is true that if a system is controllable, it is stabilizable, but the reverse is not always true. There are cases where a system is stabilizable but not controllable.
For example, if A is stable and B is a zero vector, the system's stability is maintained even with a suitable K, but it is not controllable, and it is not possible to arbitrarily place poles.
If a system is controllable, poles of (A-BK) can be arbitrarily placed by giving an appropriate feedback gain K.

As shown in the figure, the controllability matrix Uc is used to check controllability. This matrix U_c is constructed with B, AB, ... arranged in sequence. If the rank of this matrix is n, the system is controllable.
Controllability Matrices by Order
First, in the case of n = 1, the number of states is 1, and U_c takes the following form:
\begin{equation} U_c = B\end{equation}
If B is non-zero, the system with n = 1 is controllable.
Next, in the case of n = 2, the number of states is 2, and U_c takes the following form:
![]()
Finally, in the case of n = 4, U_c is given by the following:
![]()
When the number of inputs is 1, the matrix size is n \times n. If the rank is n, the system is controllable; otherwise, it is uncontrollable.
Next, let's look at specific examples.

Example 1: First, consider an one-input system with A and B matrices given as shown on the left in the figure, with n = 3. It is a second-order system, and since the rank of the controllability matrix U_c is 3, it is controllable.
Example 2: Next, consider the example where A and B are given as shown in the right of the figure with n = 3. In this case, the system's order is 3. Since the rank of the controllability matrix is 3, it is controllable. In this case, the pair of matrices A, B is in a form known as the controllable canonical form.
Observability of the State Equation
Next, I will explain observability. If a system is observable or detectable, all states of the control object can be estimated by a state observer. As with the controllable case earlier, if a system is observable, it is detectable. Conversely, if it is detectable, it is not necessarily observable.

To check observability, the observability matrix should be examined. This observability matrix is constructed with arranged vertically.
Observability Matrices by Order
First, in the case of , the number of states is 1, and
takes the following form:
![]()
If is non-zero, the system is observable.
Next, in the case of , the number of states is 2, and
takes the following form:

Finally, in the case of , the number of states is 3, and
takes the following form:
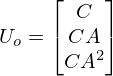
If the rank of this matrix is , the system is observable; if it is less than
, it is unobservable. Though not shown here, observable systems have an observable canonical form, just as controllable systems have a controllable canonical form.
As with the controllability matrix, if the number of outputs is 1, the matrix is square, but if the number of outputs is 2 or more, the matrix becomes tall.
Next, let's look at specific examples.

Videos Related to Controllability and Observability
Finally, I will provide a video related to observability to conclude.